El cálculo de la constante de Madelung

/ Danilo Roccatano

To all the Spanish-speaking readers, this is an AI-assisted translation experiment using WordPress. Please bear with me as my knowledge of the Spanish language is limited, so I cannot detect possible incorrect translations of the original test in Italiano. If you appreciate my efforts, please let me know. If you notice any errors in the translation, please send me a message to correct them. You can find my original versions in English, Italian, and German  language of this text by clicking the links.

Estimados lectores de habla hispana, este es un experimento de traducción asistida por IA utilizando WordPress. Les pido paciencia ya que mi conocimiento del idioma español es limitado, por lo que no puedo detectar posibles traducciones incorrectas del texto original en italiano. Si aprecian mis esfuerzos, por favor háganmelo saber. Si notan algún error en la traducción, por favor envíenme un mensaje para corregirlo. Pueden encontrar las versiones originales en inglés, italiano y alemán de este texto haciendo clic en los enlaces.

En un artículo anterior (in italiano) se mostró que el término electrostático de la energía reticular de un cristal contiene un factor (A) que depende del tipo de red cristalina. Ahora examinaremos más detalladamente cómo calcular este término y su valor para un sistema iónico simple.

La energía potencial total de un cristal iónico es igual a la suma de las contribuciones de interacción electrostática del tipo

\displaystyle V_{AB} = \frac{e^2}{4\pi\epsilon_0} \frac{Z_AZ_B}{r_{AB}} \hfill (1)

La carga específica de los iones (A, B) se denota como q_A=eZ_A y q_B=eZ_B (donde $e$ representa el valor de la carga elemental y Z_{A,B} representa la carga neta del ión), separados por la distancia r_{AB}.

La suma se extiende a todos los pares de iones presentes en el sólido para cualquier estructura cristalina. La suma definida de esta manera converge muy lentamente. De hecho, si el átomo central considerado es positivo, los primeros vecinos contribuirán con un término negativo relevante, los segundos vecinos con un término positivo (repulsivo) ligeramente más pequeño, y así sucesivamente. De esta manera, el efecto global de la suma hará que la atracción entre los cationes y los aniones predomine y brinde una contribución favorable (negativa) a la energía del sólido. Veamos en detalle cómo se calcula esta suma en el caso de configuraciones de red simples, como el oro.

Reticolo monodimensionale Infinito.

En una red unidimensional con cationes y aniones alternados a intervalos constantes de longitud d, y con {q_A = +Ze} y {q_B = -Ze}, la energía potencial de interacción de un ión con todos los demás es proporcional a una serie del tipo:

V = -\frac{2Z^2}{d} + \frac{2Z^2}{2d} - \frac{2Z^2}{3d} + \frac{2Z^2}{4d} - ...

= -\frac{2Z^2}{d} \left(1 -\frac{1}{2} +\frac{1}{3} -\frac{1}{4} + ... \right)

= -\frac{2Z^2}{d} \ln 2

El factor 2 proviene del hecho de que hay los mismos iones a ambos lados del ión central. La suma depende solo del tipo de retícula y de un parámetro de escala (periodo) que es la distancia entre los centros de las partículas adyacentes, {d}.

\displaystyle V = -\frac{e^2}{4\pi\epsilon_0} \frac{Z^2}{d} (2 \ln 2) \hfill (2)

En el caso unidimensional, el potencial V contiene un factor específico de la carga de los iones y la escala de la red, {\frac{Z^2}{d}}, y el factor 2\ln 2 (= 1.3862944), llamado constante de Madelung (A), que caracteriza la simetría de la red.

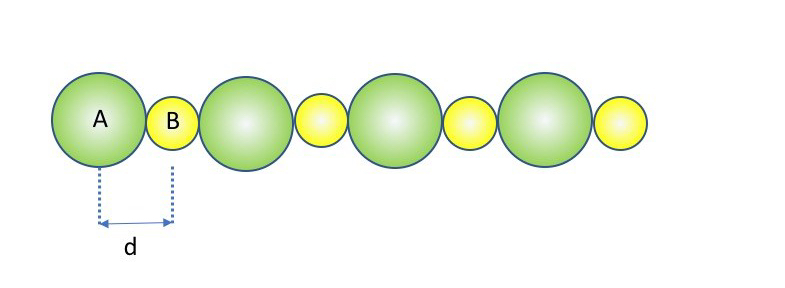
OneDimRet
Figura 1: El retículo unidimensional.

El retículo unidimensional es un modelo ideal. Recientemente, se ha logrado obtener la estructura de un cristal unidimensional de sales de sodio dentro de un nanotubo de carbono.

El Reticolo bidimensionale Infinito

En una red bidimensional, los cationes y aniones están dispuestos en los vértices de cuadrados contiguos a intervalos constantes de longitud d, y con {q_A = +Ze} y {q_B = -Ze}. En la Figura 2, considerando el ion central (1) y moviéndose radialmente desde este, la interacción de este ion con todos los demás es proporcional a una serie del tipo:

V = -\frac{4Z^2}{d} + \frac{4Z^2}{\sqrt{2} d} - \frac{8Z^2}{\sqrt{5} d} + \frac{4Z^2}{2\sqrt{2} d} + \frac{4Z^2}{2 d} ...

= -\frac{4Z^2}{d} \left(1 -\frac{1}{\sqrt{2}} +\frac{2}{\sqrt{5}} -\frac{1}{2\sqrt{2}} + \frac{1}{2 } ... \right)

reticolo2d
Figura 2: Ejemplo de un cristal iónico bidimensional ideal.

Red Tridimensional Infinita

Estos resultados pueden aplicarse a retículos tridimensionales. En los sólidos simples, la constante de Madelung es específica del tipo de cristal e independiente de las distancias interiónicas.

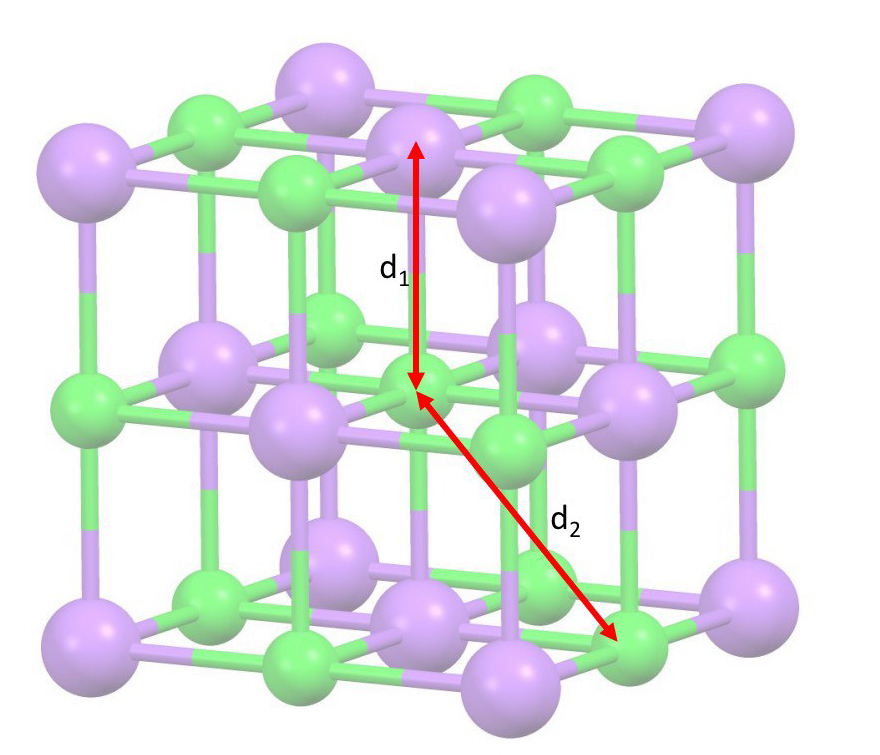
ThreeDimRetNaCl
Figura 3: Cristallo molecolare del NaCl. Le due distanze sono usate per il calcolo della costante di Madelung nel caso tridimensionale.

Para calcular la constante de Madelung para una red tridimensional, se puede seguir este proceso. Comenzando con un ión adecuado ubicado en el centro de nuestra porción de red (Figura 3), nos alejamos radialmente hasta los primeros vecinos, que serán de carga opuesta, en un número igual a {n_1} y a una distancia de {d_1}. Luego, continuamos hasta los segundos vecinos (más lejanos y de carga igual), en un número de {n_2} y a una distancia de {d_2}, y así sucesivamente. La constante de Madelung se puede expresar mediante esta suma extendida hasta el infinito.

\displaystyle A = \sum_i \left(-sgn(q_A q_B)\right) n_i \frac{1}{(d_i/d)} \hfill (3),

La fórmula {-sgn(q_A q_B)} indica que el signo de cada término de la suma es positivo si los iones tienen cargas opuestas (atracción) y negativo si tienen la misma carga (repulsión); {d=d_1} es la escala de la red (suma de los radios iónicos {r^+} + {r^-}).

Consideramos un ion Na+ en NaCl, por ejemplo, tiene 6 primeros vecinos Cl- (n₁ = 6) a una distancia d₁ = d; luego hay 12 segundos vecinos Na+ (n₂ = 12) a una distancia d₂ = d√2; luego hay 8 terceros vecinos Cl- (n₃ = 8) a una distancia d₃ = d√3, etc. Entonces, tenemos la serie:

\displaystyle A = + 6 - \frac{12}{\sqrt 2} + \frac{8}{\sqrt 3} - ... \hfill (4)

La energía potencial total por mol de fórmula en una estructura cristalina arbitraria es:

\displaystyle V = - A N_A \frac{e^2}{4\pi\epsilon_0} \frac{Z_AZ_B}{d} \hfill(5)

 StrutturaAA/n*Coordination
Cloruro di Cesio (CsCl)1.7630.88(8,8)
Salgemma (NaCl)1.7480.87(6,6)
Fluorite (CaF{_2})2.5190.84(8,4)
Solfuro di Zinco Wurtzite (ZnS)1.6410.82(4,4)
 Cloruro di Cadmio (CdCl{_2})2.2440.75(6,3)
Ioduro di Cadmio (CdI{_2})2.1910.73(6,3)
Ossido di Alluminio o Curundum (Al_2O_3)4.1720.83(6,4)
Diossido di titanio o Rutile (TiO_2)2.4080.80(6,3)
*n es el número de iones por fórmula.

La constante de Madelung aumenta con el incremento del número de coordinación. De hecho, la contribución más relevante proviene de los primeros vecinos. Los valores para la estructura NaCl (6,6) y para la estructura tipo CsCl (8,8) ilustran esta tendencia.

Si quieres leer más sobre estructuras cristalinas y su energética, entonces podrías estar interesado en estos dos artículos:

Si has encontrado interesante y útil mi artículo, no olvides darle “Like it” y suscribirte para recibir actualizaciones sobre nuevos contenidos.

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.