Il girasole piega a occidente
e già precipita il giorno nel suo
occhio in rovina … 
from the poem  “Quasi un madrigale” by Salvatore Quasimodo.

It is summer and we are delighted by the sight of the magnificent flower of Helianthus in our gardens or countryside fields. Recently, I had the chance to talk about the mathematical geometry of the sunflower’s inflorescence in an outreach lecture on the patterns and shapes in nature.  It is not a surprise that this plant was one of the topics of my lecture as it is a classic model for studying phyllotaxis and its relation with the Fibonacci numbers and logarithm spirals. Its flower, in particular, discloses numerous mathematical relations. For example, the petals of the flowers count in the Fibonacci numbers of 55, 89 or 144 (see Figure 1).

In addition, its florets (flower seeds) are also arranged in two sets of intertwining clockwise and anti-clockwise spirals (or parasthynchis) typically counting in Fibonacci numbers of 21 and 34 (for small capitulum) up to 89 and 144 for large ones, respectively.

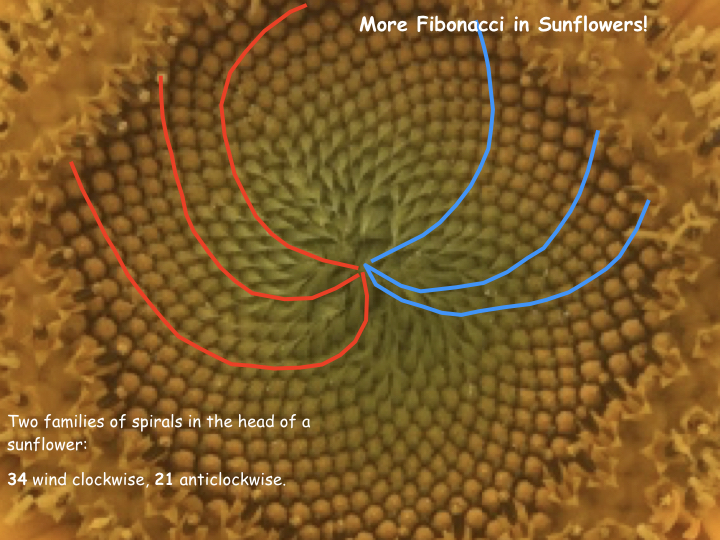
The arrangement of the florets is particularly interesting since they are packed to optimize the available space of the central disk. A simple planar model of this disposition was proposed in a paper by H. Vogel, and it is usually used to show how forms in Nature are strictly connected with properties of number, in this case, the golden number.

The Vogel model is described in the following slides:

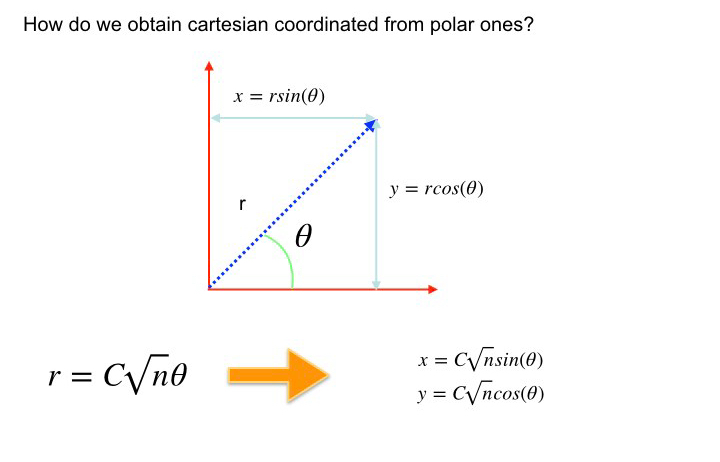
The tightly wounded spiral observed for the angle Ω=137.5 degrees was already noticed by German mathematician G. van Iterson in his pioneering work in 1907 where he showed that if you closely pack successive points separated by this angle on tightly wound spirals, then the eye would pick out one family of spiral patterns winding clockwise and one counterclockwise. The following figure shows how the angle is connected to the golden ratio.

In 1982, Ridley has rigorously proved using continuous fractions that the value of the angle equal to (recall that )  gives the most efficient packing.

I have also written a small program in Tcl/Tk language to explore the Vogel’s model.

The following PDF contains the source code: Sunflowers1.

The following GIF picture should be located in the same folder of the program.

If you have found interesting and useful my article, do not forget to press “Like it” and subscribe for updates on new ones!

BIBLIOGRAPHY

1. J.A. Adam. Mathematics in Nature. (2003). Princeton University Press.
2. M. Livio. The golden ratio. (2002).
3. I. Stewart. The mathematics of life. (2011)
4. H. Vogel. A better way to construct the sunflower head. Mathematical Bioscience. 44: 179-189. (1979).
5. J.N. Ridley. Packing efficiency in Sunflower Heads. Mathematical Bioscience. 58, 129-139 (1982).
6. TCL/TK PROGRAMMING RESOURCES