This article describes a new function of the LiStaLiA library. As I mentioned in Part I of this series of articles, I didn’t extensively test the library, so I am releasing it as an alpha version. Please let me know if you find any errors or if you improve the function, and feel free to send me your modified code!
CALCULATING STATISTICS PROPERTIES OF DATA SETS
The new functions perform a statistical analysis of the data set read by the function ReadData(). The source code of this new library functions is reported in the Appendix. The following list report all the descriptor calculated buy the functions.
- Minimum value:
The minimum value represents the smallest observation or data point in a given dataset. It indicates the lowest value among all the values in the dataset.
- Maximum value:
The maximum value refers to the largest observation or data point in a dataset. It represents the highest value among all the values in the dataset.
- First momentum or Arithmetic Mean:
The arithmetic mean, also known as the average, is calculated by summing up all the values in a dataset and dividing the sum by the total number of values. It provides a measure of the central tendency of the dataset.
- Geometric Mean:
The geometric mean is a type of average that is calculated by taking the nth root of the product of n values in a dataset. It is commonly used when dealing with values that are multiplied together, such as growth rates or investment returns.
- Harmonic Mean:
The harmonic mean is another type of average calculated by dividing the total values in a dataset by the sum of their reciprocals. It is often used when rates or ratios are involved, such as calculating average speed or average rates of return.
- Second Momentum or variance:
The second momentum, also known as the second central moment, is a measure of the dispersion or spread of the dataset around the mean. It is commonly calculated as the variance, quantifying the average squared deviation from the mean.
- Third Momentum or Skewness:
Skewness is a statistical measure that quantifies the asymmetry of a dataset’s distribution. It indicates whether the data is skewed to the left (negative skewness) or to the right (positive skewness) relative to the mean.
- Fourth Momentum or Kurtosis:
Kurtosis is a statistical measure that quantifies the peakedness or flatness of a dataset’s distribution. It provides information about the distribution’s tails and can indicate whether the dataset has heavy tails (leptokurtic) or light tails (platykurtic) compared to a normal distribution.
These statistical properties provide valuable insights into a dataset’s characteristics, central tendency, dispersion, skewness, and shape, enabling researchers and analysts to understand and analyze the data better.
HOW TO USE IT
I will show a simple example of how the functions can be used. The functions can be copied either in the main program or better in a separate file in the same or in a specified directory using the shell variable AWKPATH using the command (in bash shell)
export AWKPATH="$HOME/myawklib/LiStLA"
I suggest you to use as file name extension .awkl (or similar) to recall you that it contains a library function.
We now write a main program as a BEGIN {} block.
@include "LiStLa.awkl"
#Test driver
BEGIN {
filename="test.csv"
skipchr="#|@|;"
range[0]=1
range[1]=2
range[2]=2
range[3]=5
ReadData(filename,",",skipchr,0,range,ndata,data)
print "======================================================"
print "=============STATISTICAL ANALYSIS =================="
print "======================================================"
printf "# Data Sets : %5d\n", ndata[0]
printf "# Data Points in each set: %5d\n", ndata[1]
for (i=0;i<ndata[1];i++) {
for (n=0;n<ndata[0];n++) {
printf "%12.3f ", data[n,i]
}
printf "\n"
}
CalcProperties(ndata,data,sums,means,minmax)
CalcMu(m,ndata,data,sums,mu)
CalcQuartiles(ndata,data,quart)
print "======================================================"
for (n=0;n<ndata[0];n++) {
printf "DATA SET : %5d\n",n+1
printf "Minimum value : %12.5f\n", minmax[n,0]
printf "Maximum value : %12.5f\n", minmax[n,1]
printf "Arithmetic Mean : %12.5f\n", means[n,0]
printf "Geometric Mean : %12.5f\n", means[n,1]
printf "Harmonic Mean : %12.5f\n", ndata[1]/(sums[n,3])
printf "First Momentum : %12.5f\n", means[n,0]
printf "Second Momentum : %12.5f\n", mu[n,0]
printf "Third Momentum : %12.5f\n", mu[n,1]
printf "Fourth Momentum : %12.5f\n", mu[n,2]
printf "Skewness : %12.5f\n", mu[n,1]/(mu[n,0]^(1.5))
Kurt=mu[n,2]/(mu[n,0]^2)
eKurt=Kurt-3
printf "Kurtosis : %12.5f\n", Kurt
if (abs(eKurt) < 1e-8) {print "The distribution is Mesokurtic."}
else if (eKurt < 0) {print "The distribution is Platykurtic."}
else if (eKurt > 0) {print "The distribution is Platykurtic."
}
for (k=0;k<3;k++) {
printf "Quartile %2d : %12.5f\n", k+1,quart[n,k]
}
print "======================================================"
}
}
The script start by including the library file containg the function ReadData() using the command:
@include "LiStLa.awkl"
Inside the BEGIN block, the variable filename is set with the name of the file to analyze. To pass the file name using the command line then the variable filename need to be set to the contents of awk variable ARGV[1]. In this case a check on the number of command line argument can also be added to avoid usage mistakes.
The data content of the test.csv file is the same as in the first part of this series of articles. This script will then perform a statistical analysis of data stored in the CSV file. Let’s break down the script step by step:
- Calls the
ReadDatafunction to read data from “test.csv” using a comma (,) as the field separator and skip characters specified inskipchr. - Prints a header for the statistical analysis section.
- Several functions are called within the script:
CalcProperties: Calculates properties like sums, means, and min-max values.CalcMu: Calculates moments (first, second, third, and fourth) and skewness for each data set.CalcQuartiles: Calculates quartiles for each data set.
- Data Set Analysis Loop that iterates through each data set, performing the following calculations and printing the results:
- Minimum and maximum values
- Arithmetic, geometric, and harmonic means
- First, second, third, and fourth moments
- Skewness
- Kurtosis (with a classification message)
- Quartiles (Q1, Q2, Q3)
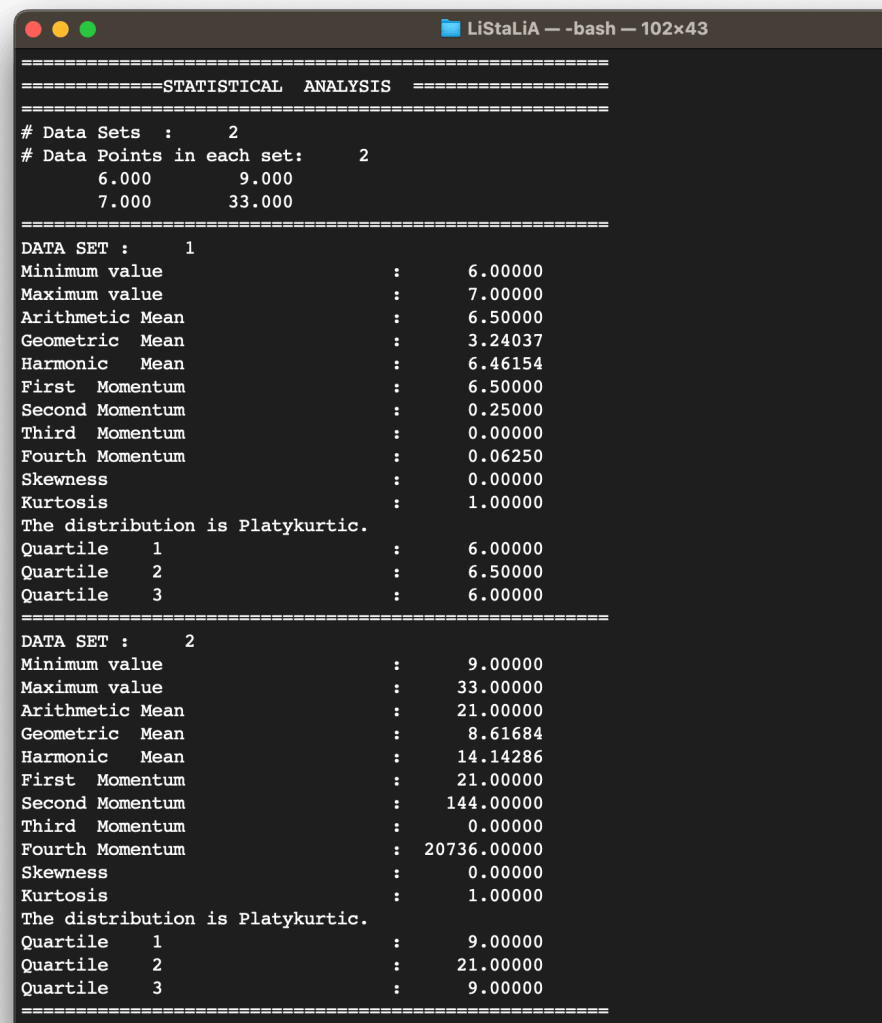
In the following figure si reported the output obtained running the test script. The program read and then print on the screen the contents of the two data sets.
IF YOU LIKE THIS ARTICLE AND YOU WANT TO KEEP INFORMED ABOUT NEW ARTICLES THEN PLEASE REPOST IT AND SUBSCRIBE MY BLOG.
APPENDIX
Previous article on Awk programming
Awk Programming II: Life in a Shell
Awk Programming III: the One-Dimensional Cellular Automaton
LIBRARY FUNCTION
This appendix contains the source codes of the functions CalcMu, CalcProperties(), CalcQuartiles(), abs().
function CalcMu(m,ndata,data,sums,mu){
#======================================================================
# FUNCTION NAME: CalcMu(m,ndata,data,sums,mu)
#======================================================================
# DESCRIPTION:
# Calculate momenta of data sets using the direct method
#
# INPUT DATA:
# m >1 : highest momentum of the distribution
# sums[n,0] : sum of the nth data set
# sums[n,1] : sum of the square of the nth data set
#
# OUTPUT DATA:
# mu[n,0] : second momentum (standard deviation) of set nth
# mu[n,1] : third momentum (skewness) of set nth
# .....
# mu[n,m] : mth momentum (skewness) of set nth
#
#==================================================================
# (c) Danilo Roccatano 1987-2020
#==================================================================
for (n=0;n<ndata[0];n++) {
sums[n,0]=0.0
}
for (i=0;i<ndata[1];i++) {
mu[n,0]=sums[n,0]/ndata[1]
for (n=0;n<ndata[0];n++) {
mu[n,0]+=(data[n,i]-means[n,0])^2
mu[n,1]+=(data[n,i]-means[n,0])^3
mu[n,2]+=(data[n,i]-means[n,0])^4
}
}
for (n=0;n<ndata[0];n++) {
mu[n,0]=mu[n,0]/ndata[1]
mu[n,1]=mu[n,1]/ndata[1]
mu[n,2]=mu[n,2]/ndata[1]
}
}
function CalcProperties(ndata,data,sums,means,minmax){
#======================================================================
# FUNCTION NAME: CalcProperties(ndata,data,sums,means,minmax)
#======================================================================
# DESCRIPTION:
# Calculate extreme and average properties for each set.
#
# OUTPUT DATA:
# sums[n,0] : sum of the nth data set
# sums[n,1] : sum of the square of the nth data set
# sums[n,3] : harmonic sum of the nth data set
# sums[n,4] : sum of the inverse of the nth data set
# means[n,0] : arithmetic means of the nth data set
# means[n,1] : geometric means of the nth data set
# means[n,2] : harmonic means of the nth data set. Note that
# if one data point is zero the value will be set to
# zero.
# minmax[n,0] : min value in the nth set
# minmax[n,1] : man value in the nth set
#================================================================-=
# (c) Danilo Roccatano 1987-2020
#================================================================-=
for (n=0;n<ndata[0];n++) {
sums[n,0]=0.0
sums[n,1]=0.0
sums[n,2]=1.0
sums[n,3]=0.0
minmax[n,0]=1e38
minmax[n,1]=-1e38
}
for (i=0;i<ndata[1];i++) {
for (n=0;n<ndata[0];n++) {
sums[n,0]+=data[n,i]
sums[n,1]+=(data[n,i]*data[n,i])
sums[n,2]*=data[n,i]
if (data[n,i] != 0 || data[n,i] !~ " ") {
sums[n,3]+=1.0/data[n,i]
} else {
sums[n,3] =0.0
}
if (data[n,i] < minmax[n,0]) minmax[n,0]=data[n,i]
if (data[n,i] > minmax[n,0]) minmax[n,1]=data[n,i]
}
}
for (n=0;n<ndata[0];n++) {
means[n,0]=sums[n,0]/ndata[1]
means[n,1]=sums[n,2]^(1./ndata[1])/ndata[1]
if (sums[n,3] !=0.0) {
means[n,2]=ndata[1]/(sums[n,3])
}else {
means[n,2]=0.0
}
}
}
function CalcQuartiles(ndata,data,quart) {
#======================================================================
# FUNCTION NAME: CalcQuartiles(ndata,data,quart)
#======================================================================
# DESCRIPTION:
# Calculate the quartiles of the data sets
# INPUT DATA:
# ndata[0] : number of data sets
# ndata[1] : number of data points
# data[n,m] : mth data point of the nth set (starting from
# data[0,0]
#
# OUTPUT DATA:
# quart[n,0] : first quartile
# quart[n,1] : second quartile (median)
# quart[n,2] : third quartile
#================================================================-=
# (c) Roccatano 1987-2020
#================================================================-=
hn=ndata[1]/2.0
ihn=int(hn)
hq=hn/2.0
ihq=int(hq)
for (n=0;n<ndata[0];n++) {
for (i=0;i<ndata[1];i++) {
a[i]=data[n,i]
}
# sort the data
asort(a,tmp)
# for (i=1;i<=ndata[1];i++) {
# print tmp[i]
# }
# Evaluate the Median (2nd quartile)
if (hn != ihn) {
quart[n,1]=tmp[ihn+1]
}else {
quart[n,1]=(tmp[ihn]+tmp[ihn+1])/2
}
# Evaluate the 1st and 3rd Quartile
if (hq != ihq) {
quart[n,0]=tmp[ihq+1]
quart[n,2]=tmp[3*ihq+1]
}else {
quart[n,0]=(tmp[ihq]+tmp[ihq+1])/2
quart[n,2]=(tmp[3*ihq]+tmp[3*ihq+1])/2
}
}
}
function abs(a) {
#======================================================================
# FUNCTION NAME: abs(c)
#======================================================================
# DESCRIPTION:
# return the absolute value of Absolute value of a
#================================================================-=
# (c) Roccatano 2020
#================================================================-=
return a>0?a:-a
}
