The game of Life was invented in the ’70 by the prolific mathematician John H. Conway (on the 11/4/2020 sadly J.H. Conway passed away at the age of 82 after having contracted the COVID-19, see [5] for his biography). The game becomes popular after Martin Gardner described it in his famous column in the Scientific American magazine [1,2].  The game is based on cellular automata conceived by Konrad Zuse and Stanislaw M. Ulam at beginning of the ’50 and then adopted by John von Neumann for his study on self-replicating automata [2,3]. A cellular automaton is composed of interacting units (cells) arranged in a square grid. The system evolves in life cycles where each cell change status and new cells can be born, and others can survive or eventually die. The status of each cell in the next cycle is defined by the interaction with their neighbor cells according to a given set of rules. The interaction occurs with the first neighbors of each cell. As shown in Figure 1, two type of neighbor’s cells (circles) can be used, the game of Life uses the Moore type neighborhood.

Conway serendipitously invented his automaton in the same period of the birth of the micro/personal computer and Gardner’ articles foster serious and amateur research activities on the properties of this automaton. The curiosity around this automaton brings to the discovery of many peculiar behaviors in particular arrangement of cells. A collection of the discovered automaton can be found in specialized dedicated to the game of Life as the Conwaylife at http://www.conwaylife.com. More about automaton and the game of Life can be found in the comprehensive book by Stephen Wolfram [4] or on Wikipedia.

Life in a Shell

Some time ago, I wrote a yet-another-life-program in awk language to visualize the evolution of Life on a terminal screen (see Appendix). This program is just an exercise to explore other features of the awk language. It is limited in graphics and in performances compared to the many existing programs of the game of Life but it is still a useful tool to explore this fascinating subject. In addition, for those having good memories of the microcomputing revolution of the ’80,  it also gives a retro-computing feeling!

The program read game of Life starting configurations in RLE ( run-length encoding) format. To run the program type

awk  -f Life.awk RLEfile

At the start, it gets the size of the terminal window (lines x columns) using the function TermSize() from the shell command tput. The terminal size is used to set the dimensions of the matrices used by the game. The function GenFrame() prepare the frame bordering the game arena. The type of neighbors used by the game is set using the function Neighbor(1), the parameter 1 is for Moore’s type. The function RLEreader read the contents of the RLE file and add the starting cell configuration to the center of the game matrix. The program does not read the type of rule since it only uses the original Conway rules (B3/S23). Therefore, please check the type of rule in the RLE file before using it [however, it is not difficult to implement also other types of rule by reading them from the RLE file and implementing in the function applyRule()]. The program then prints a menu that allows choosing to run the game in a continuous way by setting the number of generation or interactively by providing along the generation the number of steps to advance. The menu is set by using the do while loop (implemented in the gnu awk) and by getting the input from the keyboard using the command getline ch < “-“.  The animation is performed by printing the matrix of the game that is updated according to the Life rules every step with the character frames. The colors, cleaning of the screen is obtained using ESC characters. In Mac OSX, you can increase or decrease the size of characters used in the terminal with the Cmd+/- keys, respectively. Decreasing the size of the characters, you can then increase the number of lines and columns by enlarging the terminal window. This will give you a larger game field for a large starting configuration of the game but you will pay the price of a reduced speed of the program. If the variable PBC in the BEGIN block of the program is set to 1, the game run with periodic boundary conditions. This is equivalent to run the game on the surface of a torus. The program is provided as it is and everybody is welcome to try and if you can improve it then please send me the new version!

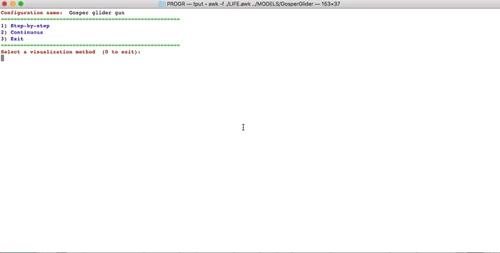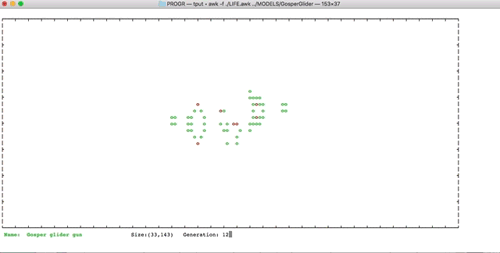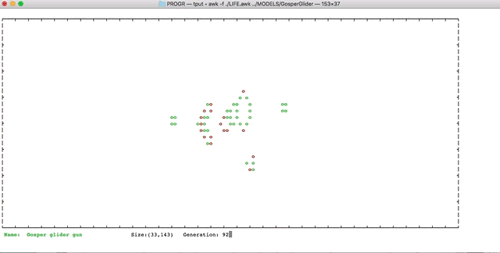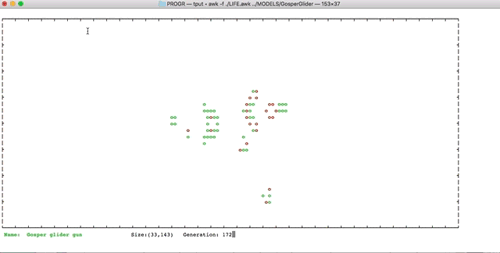
I have added some examples of well-known configurations The examples are generated using RLE file obtained from the above-cited Conwaylife website. Enjoy it!

REFERENCES

1. M. Gardner. The fantastic combination of John Conway’s new solitaire game “life”.”. Scientific American, October 1970.
2. M. Gardner. On cellular automata, self-reproduction, the Garden of Eden and the game of “life”. Scientific American, Feb. 1971.
3. M. Schroeder. Fractal, Chaos, Power Laws: minutes from an infinite paradise., Dover Ed., 1991.
4. S. Wolfram. A new kind of Science. Wolfram Media Inc.
5. S. Roberts. Genius at Play. Bloomsbury Publishing, 2015.

APPENDIX

The game was developed and tested on Mac OSX using the gawk. The program is in here:

LIFE

Please copy it to a text file named, for example, Life.awk.