Madelung定数の計算

/ Danilo Roccatano

To all Japanese-speaking readers, this text is part of an experiment using AI translation and WordPress. We kindly ask for your understanding and cooperation. If you find value in this initiative, please let us know. Additionally, if you notice any translation inaccuracies, we would greatly appreciate it if you could contact us. You can find the original text in English, Chinese, Italian, and German by clicking the links.

親愛なる日本語を話す読者の皆様へ、これはワードプレスを使用したAI翻訳の実験です。私の成長と改善にご協力いただければ幸いです。私の取り組みを評価していただける場合は、ぜひお知らせください。翻訳に誤りを見つけた場合は、修正するためにメッセージをお送りください。英語、中国語、イタリア語、ドイツ語のオリジナルテキストは、リンクをクリックすることで見つけることができます。

以前の記事で、結晶の格子エネルギーにおける静電エネルギー項の計算について説明しました。この記事では、この項を計算する方法について詳しく説明し、また単純なイオン系におけるこの項の値を提供します。

晶体の総クーロン相互作用エネルギーは、個々の相互作用項の合計として与えられます。

\displaystyle V_{AB} = \frac{e^2}{4\pi \epsilon_0} \frac{Z_AZ_B}{r_{AB}} \hfill (1)

固体の結晶構造では、電荷qAとqBを持つイオン対の間の距離rABによって生じるクーロン相互作用力で構成されます。この和は、固体中のすべてのイオン対にわたって計算されます。

最初の近傍は負の重要な寄与を提供するため、この和は非常に遅く収束します。2番目の近傍原子はわずかに弱い正の項を生成します。このプロセスは無限遠まで続き、交互の符号でますます小さい値を通じて行われます。このようにして、陽イオンと陰イオンの間の引力が主導し、固体のエネルギーに有益な負の寄与を提供します。

無限の1次元グリッド。

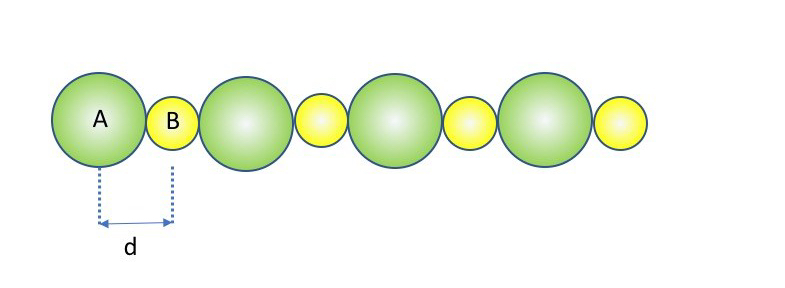
onedimret.jpg

一つの一定の間隔で配置された単一の次元ネットワークにおいて、陽イオンと陰イオンが交互に出現し、電荷量はそれぞれqA=+ZおよびqB=-Zです。イオン間の相互作用は、以下のリストで表されます：

V = -\frac{2Z^2}{d} + \frac{2Z^2}{2d} - \frac{2Z^2}{3d} + \frac{2Z^2}{4d} - ...

= -\frac{2Z^2}{d} \left(1 -\frac{1}{2} +\frac{1}{3} -\frac{1}{4} + ... \right)

= -\frac{2Z^2}{d} \ln 2

（**各イオンがそれぞれの両側に同じ数のイオンを持っているため、2の因子が生じる）。合計は、格子のタイプと隣接する粒子の中心との距離dに依存します：

\displaystyle V = -\frac{e^2}{4\pi \epsilon_0} \frac{Z^2}{d} (2 \ln 2) \hfill (2)

一次元格子の場合、\displaystyle V には電荷の種類や格子に関連する項 \frac{Z^2}{d} が含まれます。因子 2 \ln 2 (= 1.3862944) は**マーデュラン（A）**定数と呼ばれ、格子の対称性を表します。

無限の2次元グリッド

このブロックのためのいくつかのコンテンツを教えてください。

reticolo2d

2次元グリッドの場合、陽イオンと陰イオンは隣接する正方形の長さdで配置されます。ここで、$ q_A = +Z $ および $ q_B = -Z $ のように、イオン（1）を中心として他のすべてのイオンとの相互作用が次のようになります：

V = -\frac{4Z^2}{d} + \frac{4Z^2}{\sqrt{2} d} - \frac{8Z^2}{\sqrt{5} d} + \frac{4Z^2}{2\sqrt{2} d} + \frac{4Z^2}{2 d} ...

= -\frac{4Z^2}{d} \left(1 -\frac{1}{\sqrt{2}} +\frac{2}{\sqrt{5}} -\frac{1}{2\sqrt{2}} + \frac{1}{2 } ... \right)

無限の3次元のウェブ構造

[この表現は、[立体格子]にも簡単に拡張することができます]。

threedimretnacl.jpg

固体の場合、ナトリウムクロライド（NaCl）のような単純な物質では、マドラン定数は結晶のタイプとイオン間の距離に依存します。3次元格子のマドラン定数は、結晶の中心から引き離された最初の逆符号の電荷を持つ隣接イオンまでの距離（n_1個のイオン）を見つけることから計算されます（距離はd_1）。次に、イオンの中心に向かって径方向に移動し、同じ電荷を持つ中心イオンに対して第2のグループの隣接イオン（n_2個）が存在する距離（距離はd_2）を見つけることができます。それからも前のイオンの組織化された同心の殻内で同様の方法で、隣接する原子のグループを見つけることができます。この場合、マドラン定数の定義は以下の総和で表されます：

\displaystyle A = \sum_i \left(- sgn(q_A q_B) \right) n_i \frac{1}{(d_i/d)} \hfill (3),

この式では、{-sgn(q_A q_B)}は、和の各項の符号を表します。イオンが反対の電荷を持つ場合（引力）、符号は正になります。イオンが同じ電荷を持つ場合（斥力）、符号は負になります。{r^+} + {r^-}は格子内のイオンの半径の合計です。

Example

例えば、私たちはNaCl中のNa+を考えてみます。それは6つの第一近接Cl-（n1 = 6、距離d1 = d）を持っています。そして、12個の第二近接Na+（n2 = 12）の距離、8個の第三近接Cl-（n3 = 8）の距離などがあります。したがって、得られるシーケンスは以下の式で与えられます：

\displaystyle A = + 6 - \frac{12}{\sqrt 2} + \frac{8}{\sqrt 3} - ... \hfill (4)

結晶構造中の1モルあたりのポテンシャルエネルギーは：

\displaystyle V = - A N_A \frac{e^2}{4\pi \epsilon_0} \frac{Z_AZ_B}{d} \hfill(5)

StructureAA/n*Coordination
CsCl1.7630.88(8,8)
Halite (NaCl)1.7480.87(6,6)
Fluorite (CaF2)2.5190.84(8,4)
Wurtzite (ZnS)1.6410.82(4,4)
CdCl22.2440.75(6,3)
CdI22.1910.73(6,3)
Rutile (TiO_2)2.4080.80(6,3)
Curundum (Al_2O_3)4.1720.83(6,4)

T表1: いくつかの固体のマデラン定数

* これは、Aに対するイオンの数nを化学式中に含めたものです。

NaCl（6,6）やCsCl（8,8）のような構造では、マデルング定数は配位数の増加とともに増加します。これは最も重要な寄与が最初の近傍から来るためです。

もし結晶構造とエネルギー学に興味があるのであれば、以下の2つの記事がおすすめです：

如果你觉得我的文章有趣且有用，请不要忘记点击“喜欢”并订阅新文章的更新！

One thought on “Madelung定数の計算”

  1. Pingback: Madelung常数的计算 |

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.