Month: September 2023

Methods of Calculating Atomic Charges based on Electronegativity. Part I.

/ Danilo Roccatano / Leave a comment

The electronegativity of a chemical element measures the tendency of an atom to attract electrons around it. This definition was formalized for the first time, in a semi-empirical form, by the chemist Linus Pauling in the early 1930s, but it had already been proposed in the late 1800s by the Swedish chemist Berzelius. In molecules, this tendency determines the molecular electronic distribution and therefore influences molecular properties such as the distribution of partial charges and chemical reactivity. Pauling provided an electronegativity scale by comparing bond dissociation energies of pairs of atoms (A, B) using the equation

\chi_P=E_{AB}-\left(\frac{E_{AA}-E_{BB}}{2}\right)

With $E_{AB}$, $E_{AA}$, and $E_{BB}$ being the dissociation energies of the molecules AB, AA, and BB, respectively.

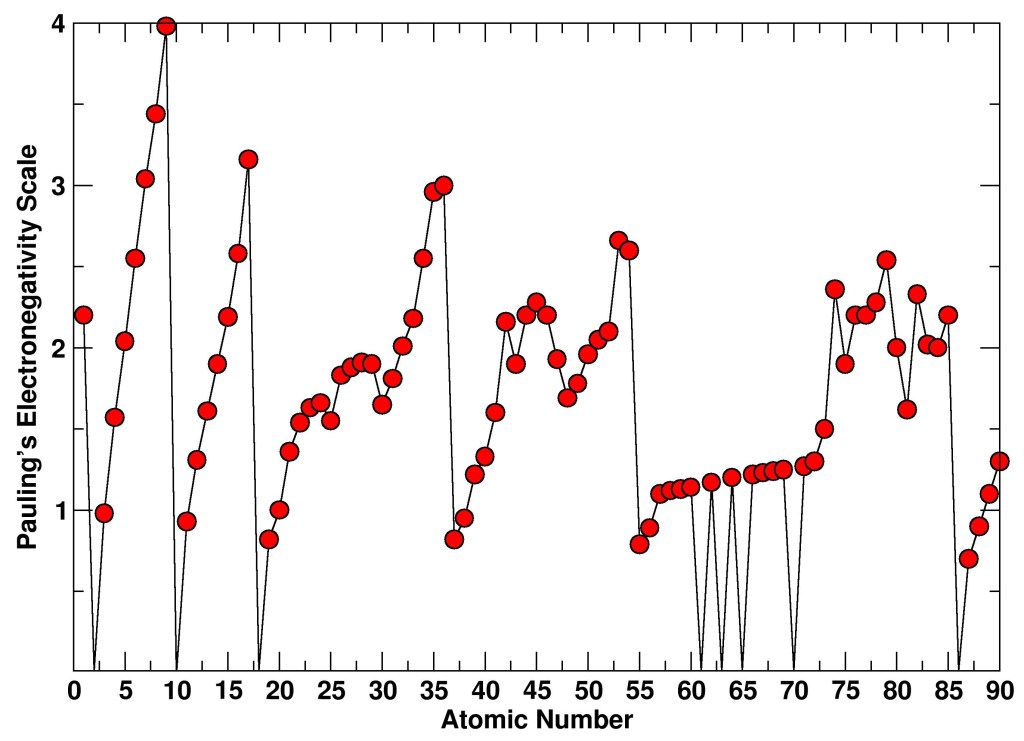
A few years later, in 1934, Mulliken proposed an expanded definition of electronegativity based on spectroscopically measurable atomic properties such as ionization potential (I) and electron affinity (E):

\chi_M=\left(\frac{I-A}{2}\right)

Continue reading →

I Metodi di Calcolo delle Cariche Atomiche basati sull’Elettronegatività. Parte I.

/ Danilo Roccatano / Leave a comment

L’elettronegatività di un elemento chimico misura la tendenza di un atomo ad attrarre intorno a sé elettroni. Questa definizione fu formalizzata per la prima volta, in foma semi-empirica, dal chimico Linus Pauling all’inizio del 1930 ma era già stata proposta nella seconda metà dell’1800 dal chimico svedese Berzelius. Nelle molecole, questa tendenza determina la distribuzione elettronica molecolare e quindi influenza le proprietà molecolari quali per esempio, la distribuzione delle cariche parziali e la reattività chimica. Pauling ha fornito una scala di elettronegatività confrontando le energie di dissociazione di legame di coppie di atomi (A, B) usando la relazione

\chi_P=E_{AB}-\left(\frac{E_{AA}-E_{BB}}{2}\right)

con E_{AB}, E_{AA}, and E_{BB}, rispettivamente le energie di dissociazione delle molecole AB, AA, and BB.

Qualche anno dopo, nel 1934, Mulliken propose una definizione estesa di elettronegatività basata su proprietà atomiche misurabili spettroscopicamente, quali il potenziale di ionizzazione (I) e l’affinità elettronica (E):

\chi_M=\left(\frac{I-A}{2}\right)

Continue reading →

Retro Programming Nostalgia V: Phase Plane of Autonomous Planar System of DE

/ Danilo Roccatano / Leave a comment

What is the origin of the urge, the fascination that drives physicists, mathematicians, and presumably other scientists as well? Psychoanalysis suggests that it is sexual curiosity. You start by asking where little babies come from, one thing leads to another, and you find yourself preparing nitroglycerine or solving differential equations. This explanation is somewhat irritating, and therefore probably basically correct. David Ruelle, in Chance and Chaos

Here I am again for a new appointment with the Italian version of the column “Retro Programming Nostalgia“, my very own adventure in computer archaeology, rediscovering old programs written some time ago on microcomputers that have made their mark on an era.

This time, in my old floppy disks for the glorious Amiga 500, I found a program in Amiga Basic that I wrote during the early years of my university studies, when I was taking the course on differential equations II. Specifically, I was very fascinated by autonomous systems of differential equations due to their numerous applications in mathematical modeling of physical, chemical, and biological systems, as well as their importance in the theory of chaos. As in the series articles, I want to release an adapted version for the QB64 BASIC meta-compiler, but before presenting the program, I want to briefly explain what an autonomous system of differential equations is.

Continue reading →

Retro Programming Nostalgia V: Sistemi Autonomi di Equazioni differenziali

/ Danilo Roccatano / Leave a comment

“Qual è l’origine del desiderio, della fascinazione che spinge i fisici, i matematici e presumibilmente anche altri scienziati? La psicoanalisi suggerisce che si tratti di curiosità sessuale. Si comincia chiedendosi da dove vengano i bambini piccoli, una cosa porta all’altra e ci si ritrova a preparare il nitroglicerina o a risolvere equazioni differenziali. Questa spiegazione è un po’ irritante, e quindi probabilmente fondamentalmente corretta.” – David Ruelle, in “Chance and Chaos”

Eccomi di nuovo per un nuovo appuntamento con la versione in italiano della Rubrica “Retro Programming Nostalgia “, la mia personalissima avventura d’ archeologia informatica alla riscoperta di vecchi programmi scritti qualche tempo fa su microcomputers che hanno segnato un’epoca.

Questa volta, nei miei vecchi dischetti per il glorioso Amiga 500, ho trovato un programma in Amiga Basic che scrissi durante i primi anni dei miei studi universitari, quando studiavo nel corso di matematica II, i sistemi d’equazioni differenziali. In particolare, ero molto affascinato dai sistemi di equazioni differenziali autonomi per via delle molteplici applicazioni nella modellazione matematica di sistemi fisici, chimici e biologici, e per la loro importanza nella teoria del caos. Come negli articoli della serie, voglio rilasciare una versione riadattata per il meta compilatore QB64 BASIC, ma prima di presentare il programma, voglio brevemente spiegare cosa sia un sistema autonomo di equazioni differenziali.

Continue reading →

Programming in Awk Language. LiStaLiA: Little Statistics Library in Awk. Part II

/ Danilo Roccatano / Leave a comment

This article describes a new function of the LiStaLiA library. As I mentioned in Part I of this series of articles, I didn’t extensively test the library, so I am releasing it as an alpha version. Please let me know if you find any errors or if you improve the function, and feel free to send me your modified code!

CALCULATING STATISTICS PROPERTIES OF DATA SETS

The new functions perform a statistical analysis of the data set read by the function ReadData(). The source code of this new library functions is reported in the Appendix. The following list report all the descriptor calculated buy the functions.

Continue reading →

Madelung定数の計算

/ Danilo Roccatano / 1 Comment

To all Japanese-speaking readers, this text is part of an experiment using AI translation and WordPress. We kindly ask for your understanding and cooperation. If you find value in this initiative, please let us know. Additionally, if you notice any translation inaccuracies, we would greatly appreciate it if you could contact us. You can find the original text in English, Chinese, Italian, and German by clicking the links.

親愛なる日本語を話す読者の皆様へ、これはワードプレスを使用したAI翻訳の実験です。私の成長と改善にご協力いただければ幸いです。私の取り組みを評価していただける場合は、ぜひお知らせください。翻訳に誤りを見つけた場合は、修正するためにメッセージをお送りください。英語、中国語、イタリア語、ドイツ語のオリジナルテキストは、リンクをクリックすることで見つけることができます。

以前の記事で、結晶の格子エネルギーにおける静電エネルギー項の計算について説明しました。この記事では、この項を計算する方法について詳しく説明し、また単純なイオン系におけるこの項の値を提供します。

晶体の総クーロン相互作用エネルギーは、個々の相互作用項の合計として与えられます。

\displaystyle V_{AB} = \frac{e^2}{4\pi \epsilon_0} \frac{Z_AZ_B}{r_{AB}} \hfill (1)

固体の結晶構造では、電荷qAとqBを持つイオン対の間の距離rABによって生じるクーロン相互作用力で構成されます。この和は、固体中のすべてのイオン対にわたって計算されます。

最初の近傍は負の重要な寄与を提供するため、この和は非常に遅く収束します。2番目の近傍原子はわずかに弱い正の項を生成します。このプロセスは無限遠まで続き、交互の符号でますます小さい値を通じて行われます。このようにして、陽イオンと陰イオンの間の引力が主導し、固体のエネルギーに有益な負の寄与を提供します。

Continue reading →

Unix C-Shell Programming Notes: Part II

/ Danilo Roccatano / 1 Comment

This is the second part of this series of notes on the advanced use of the Unix shell. The first part can be accessed by following the link. In this second part, I will show some advanced examples I wrote for my research activity.

1. CHANGE FILE NAMES SCRIPT

I wrote this script to change the default names of the files generated during a molecular dynamics simulation by the program mdrun in the early version of the GROMACS package for MD simulation. GROMACS is a widely used software package for simulating the behavior of molecules and molecular systems. Although it is now possible to define the root name of the files upon running the simulation program, this script can still be helpful. The script is written in the C Shell (csh) . 

 #! /bin/csh -ef
#
# Change the names of the default  output Files
# generated by the program GROMACS mdrun program
#
# (c) Danilo Roccatano
#######
#
#Define the radix of the files name
#
setenv RADIX  'EH_min'

if (-e md.log) then
   if (  -e $RADIX'.log')  then 
     echo Warning $RADIX'.log' exist
   else
     mv md.log            $RADIX'.log'
   endif
else
   echo The md.log file does not exist!
endif

if (-e ener.ene) then
  if (  -e 'e'$RADIX'.ene') then 
   echo Warning 'e'$RADIX'.ene' exist
  else
    mv ener.ene       'e'$RADIX'.ene'
  endif
else
  echo The energy file does not exist
endif

if (-e ctraj.xtc ) then
  if ( -e 'r'$RADIX'.xtc') then 
    echo Warning 'r'$RADIX'.xtc' exist
  else
    mv ctraj.xtc      'r'$RADIX'.xtc'
  endif
else
  echo The compressed trajectory file does not exist
endif

if (-e confout.gro) then
  if ( -e 'x'$RADIX'.gro') then 
    echo Warning 'x'$RADIX'.gro' exist
  else
    mv confout.gro    'x'$RADIX'.gro'
  endif
else
  echo The final configuration file does not exit.
  echo Probably your simulation crashed before the end 
endif
 
exit
Continue reading →