Cristallo e fiamma, due forme di bellezza perfetta da cui lo sguardo non sa staccarsi

Italo Calvino, Lezioni americane. Sei proposte per il prossimo millennio.

The successful reception of my previous posts on calculating the lattice energy, the calculation of the Born-Haber cycle and the Madelung constant motivated me to write more about the crystal structures of inorganic and organic compounds. In this series of articles, I will briefly introduce the crystallography. It does not pretend to be comprehensive, but it is meant to give just a flavor of this fascinating topic.

What is a Crystal?

At the atomic level, a crystal is solid with regular arrangements of atoms in space. Depending on the material, these arrangements have different symmetry properties that generate beautiful symmetric shapes at the macroscopic level.A regular and infinite arrangement of atoms can be visualized as a vast and complex network of interconnected particles. Each atom, with its unique properties, contributes to the overall complexity and variety of the system. The repeating patterns of the atoms create an endless and fascinating display. This assembly of atoms forms the basis of the world of matter, showcasing the intricate and beautiful nature of the smallest units of our universe.
We start introducing the Bravais lattice’s fundamental concept to describe and classify these atomic arrangements..The term “Bravais lattice” is a name given to a mathematical concept used to describe how points are arranged in a crystal. It is named after Auguste Bravais, a physicist from France who studied crystals in the 19th century. Bravais introduced the idea of different types of arrangements and symmetry in crystal structures. His work was important in understanding how crystals are classified based on their symmetry. The Bravais lattice is a fundamental concept in crystallography that describes the periodic arrangement of points in a crystal lattice. It provides a framework for classifying and categorizing different types of crystal structures based on their symmetry and arrangement of lattice points.

Specifically, a Bravais lattice is an infinite array of points in three-dimensional space that can be generated by translating a single point by a set of linearly independent vectors, known as lattice vectors. These lattice vectors define the basic repeating unit, called a unit cell, of the crystal lattice. The unit cell can be thought of as a box that, when stacked together in all directions, forms the entire crystal structure.
Lattice systems are characterized by six parameters that represent the size and orientation of the lattice structure. The three basis vectors of a lattice units , and extend from a common origin in a righ-handed system along the $x$, $y$, and $z$ dimensions, respectively. The lenght of a unit cell vecor is given by its norm , and The angles , and describe the angles between the lattice vectors. Together, these parameters fully specify the lattice system. In Figure 1A, you can observe the relationships between the lattice vectors. The angle $latx \alpha$ is formed between vectors and , $\beta$ between vectors and , and between vectors and .

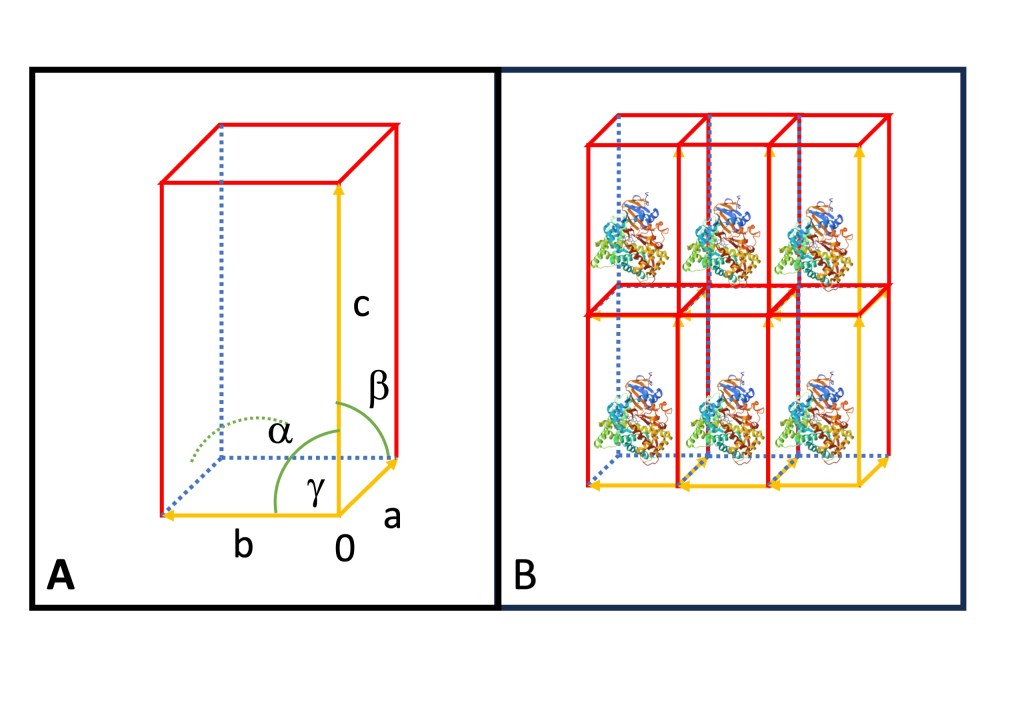
The Bravais lattice provides a fundamental framework for describing and understanding the arrangement of atoms or points in crystal structures. One can fully describe the crystal structure and symmetry properties by combining the Bravais lattice with the basis (the arrangement of atoms or groups within the unit cell, Figure 1B,).

BRAVAIS LATTICES

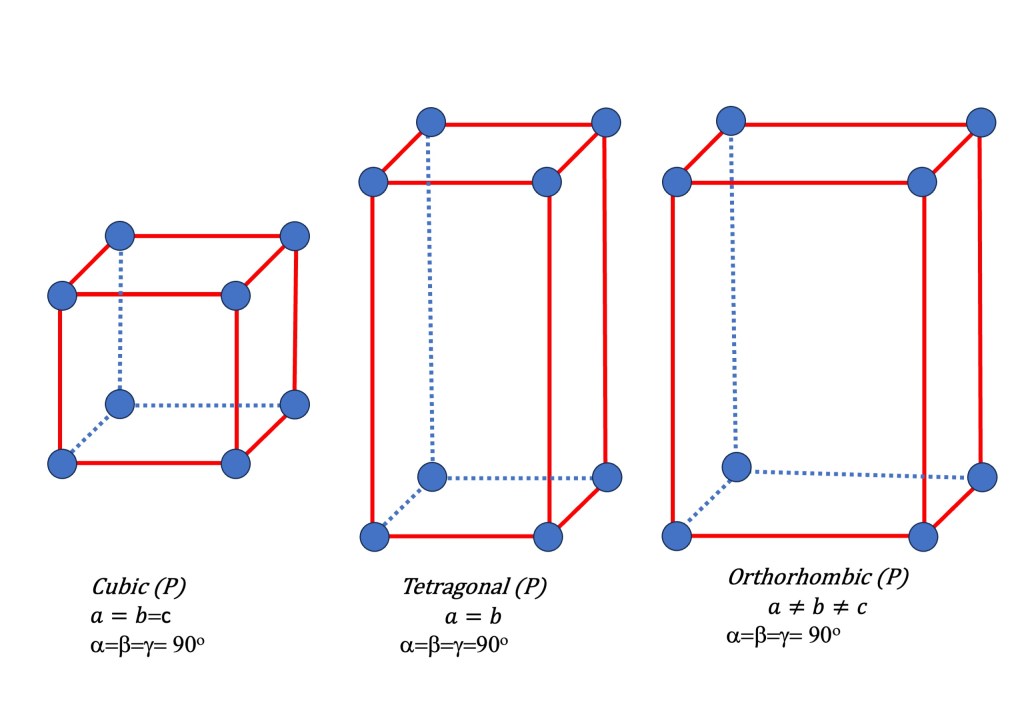
There are 7 possible Bravais primitive lattices in three dimensions. The 7 primitive lattices represent the fundamental symmetries that can occur in crystal structures. The corresponding Bravais lattices in three dimensions are:

1. Cubic (P): This lattice has equal lattice parameters (a = b = c) and all angles are 90 degrees. It is characterized by its simplicity and high symmetry.
2. Tetragonal (P): This lattice has two different lattice parameters (a = b ≠ c) and all angles are 90 degrees. It is similar to the cubic lattice but elongated along one axis.
3. Orthorhombic (P): This lattice has three different lattice parameters (a ≠ b ≠ c) and all angles are 90 degrees. It is characterized by unequal axis lengths.
4. Trigonal/ Rhombohedral, Hexagonal (P): Rhombohedral can be derived by deforming and pulling the cubic lattice along one diagonal. Therefore it has three equal lattice parameters. (a=b=c) but all angles are non-90 degrees. It forms a rhombohedron shape. It has a triangular symmetry.
5. Monoclinic (P): This lattice has three different lattice parameters (a ≠ b ≠ c) and the angles between two of the axes are 90 degrees while the third angle is variable.
6. Triclinic (P): This lattice has three different lattice parameters (a ≠ b ≠ c) and all angles are variable. It is the least symmetric lattice system.

Note that in modern representation, the trigonal lattice (originally called Rhombohedral) is used to represent the hexagonal primitive with two equal lattice parameters (a = b), and all angles are 90 degrees except for one angle, which is 120 degrees.

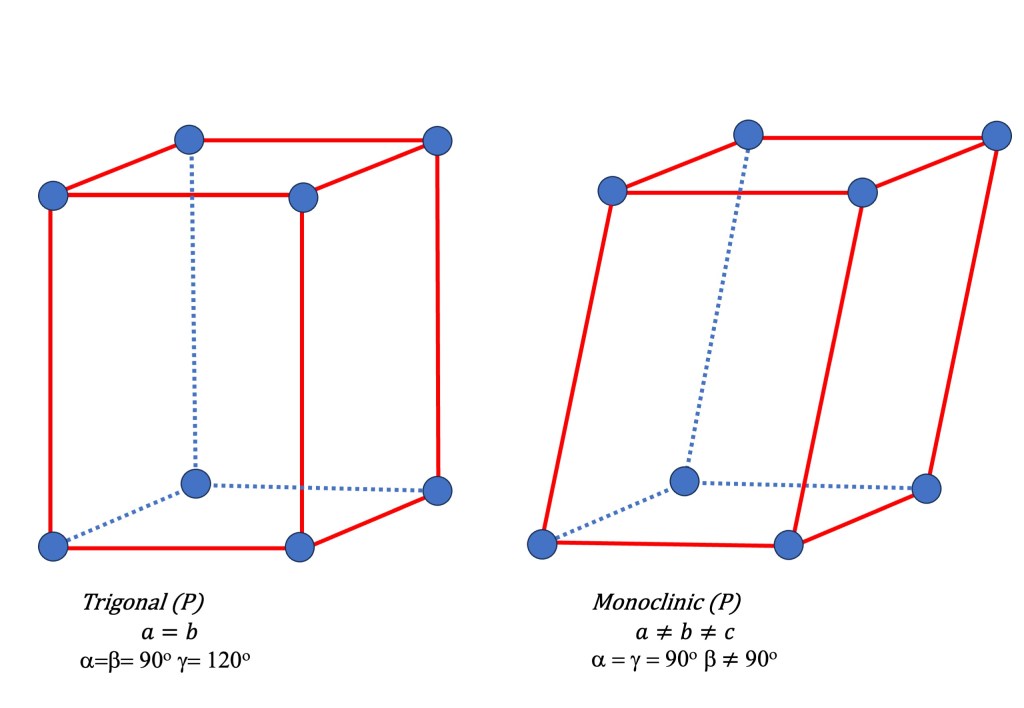
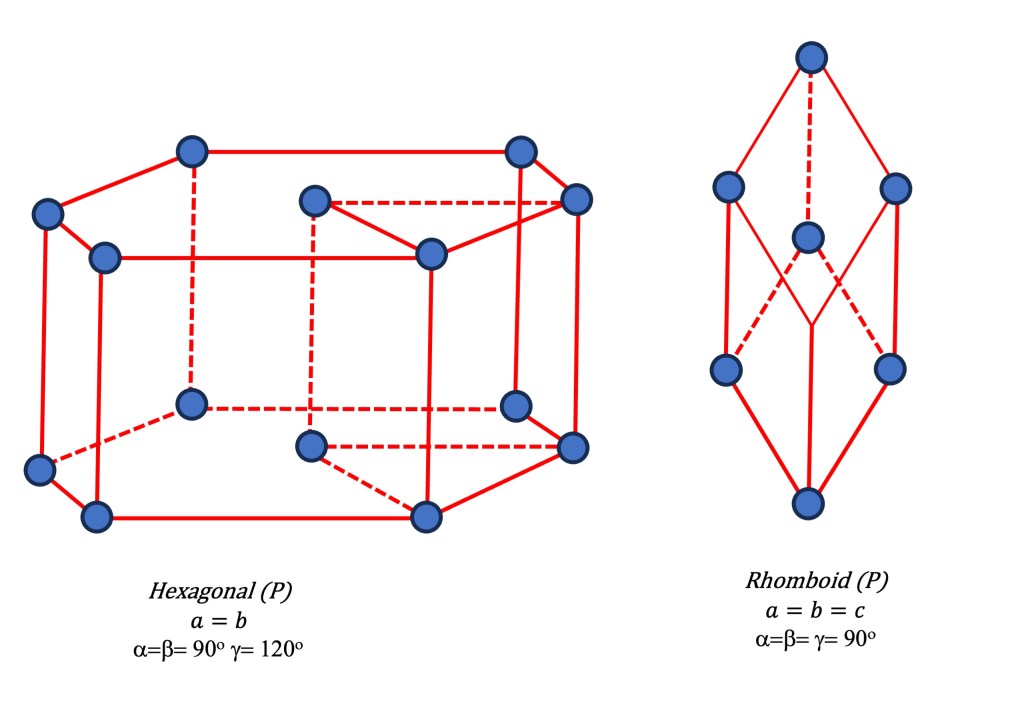
Apart from the 6 primitive lattice systems mentioned previously, eight other Bravais lattices result from combining the primitive lattices with additional symmetry operations.

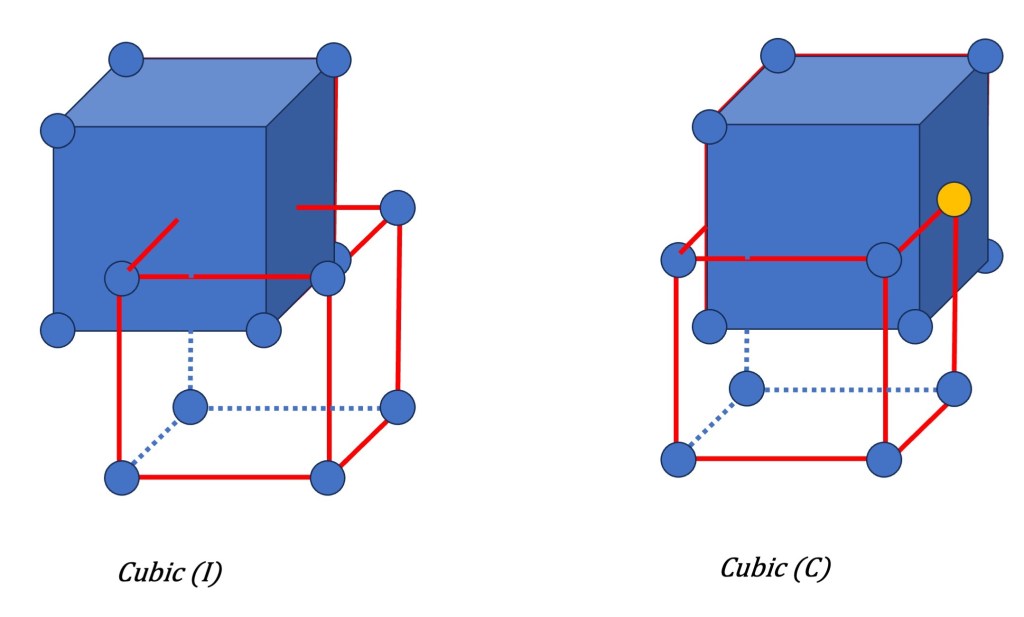
1. Body-Centered Symmetry (I): In a body-centered lattice, there is an additional lattice point positioned at the center of the unit cell in addition to the lattice points located at the corners. This symmetry results in a center of inversion, meaning that if any point in the lattice is inverted through the center, it will coincide with another lattice point. This symmetry is denoted by the symbol “I” and is one of the possible additions to the primitive lattices.
2. Face-Centered Symmetry (F): In a face-centered lattice, lattice points are not only positioned at the corners of the unit cell but also at the center of each face. By adding these additional lattice points, the symmetry of the lattice enhances. Face-centered lattices possess various symmetry elements, including mirror planes and glide reflection symmetry. The symbol “F” denotes face-centered symmetry in the Bravais lattice notation.
3. Base-Centered Symmetry (C): Base-centered symmetry is observed when lattice points are present at both the corners and the center of two opposite faces of the unit cell. This additional lattice point arrangement introduces new symmetry elements such as mirror planes and screw axes. Base-centered lattices are designated with the symbol “C” in the Bravais lattice classification.

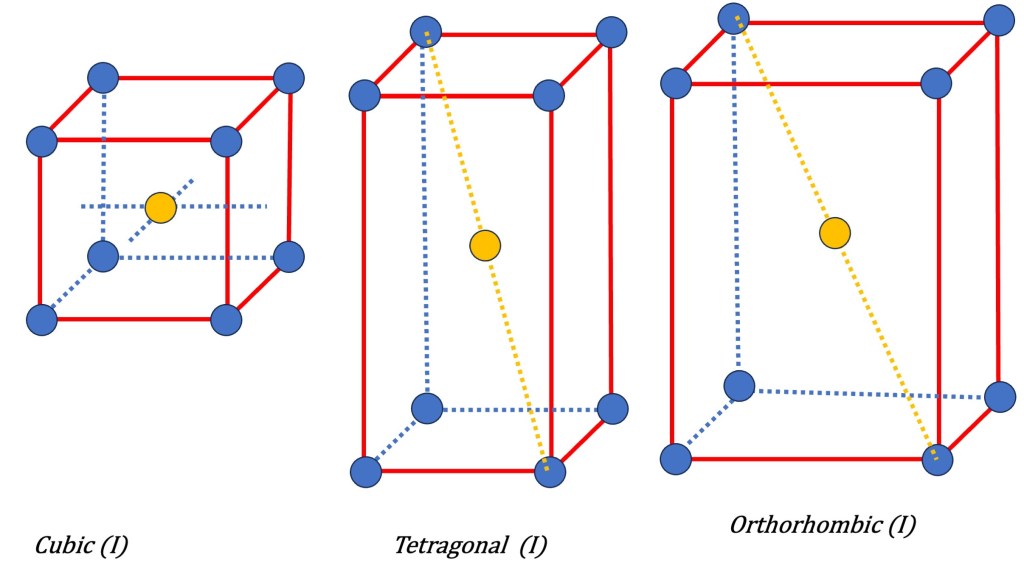
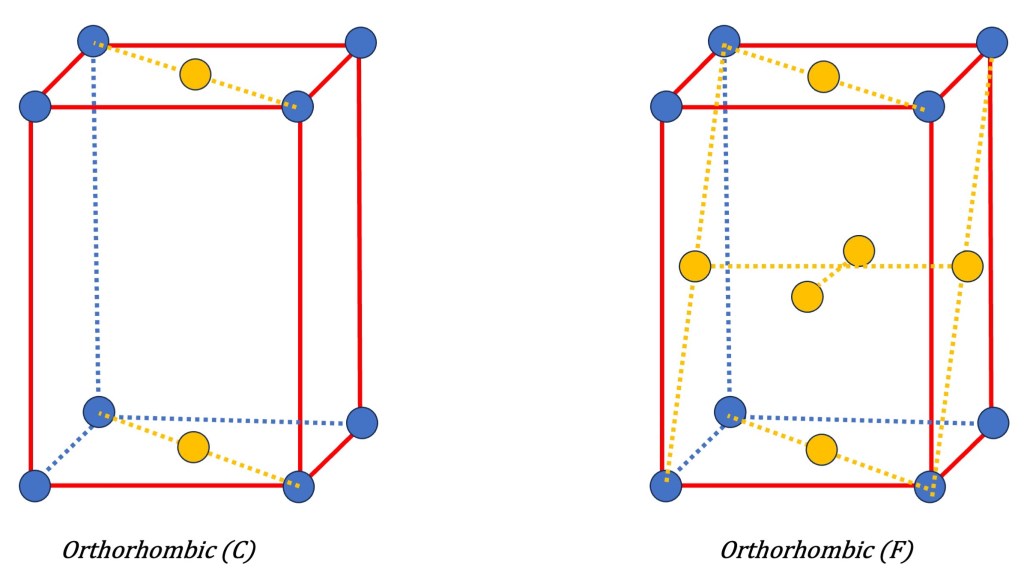
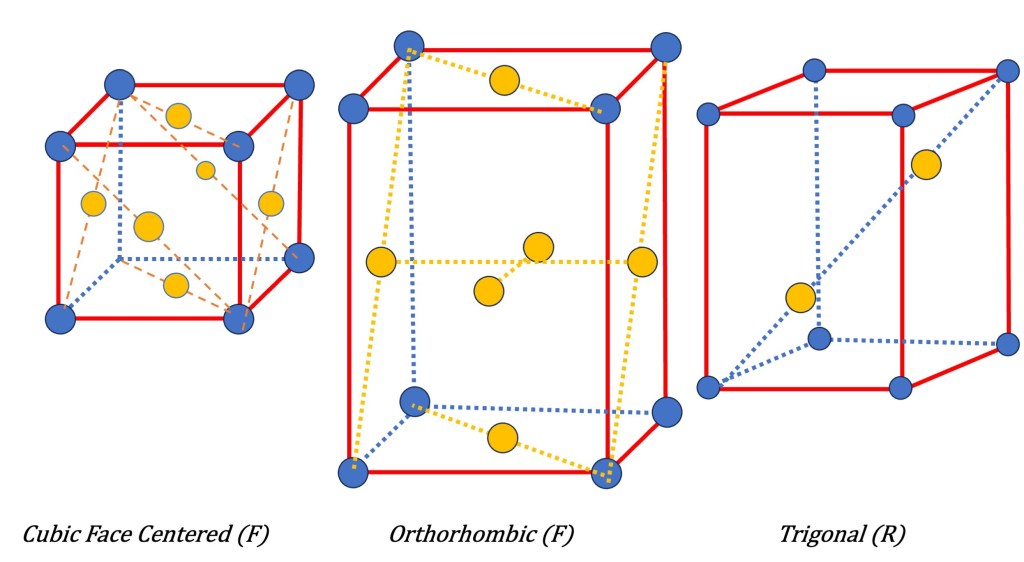
These types of additional symmetries, along with the primitive lattice symmetries, form the basis for the 14 Bravais lattices that describe the periodic arrangement of points in three-dimensional space.

REFERENCES

Atkins, P., Atkins, P.W. and de Paula, J., 2014. Atkins’ physical chemistry. Oxford university press.