Integrazione Numerica di Equazioni Differenziali: 50 anni fa l’uomo ha messo piede sulla Luna. Parte II |

Houston, Tranquillity Base here. The Eagle has landed.
Neil Armstrong

Questo è il secondo articolo di questa serie dedicata alla soluzione numerica delle equazioni differenziali. La serie prende spunto dagli eventi che hanno portato l’uomo sulla Luna.

Nel luglio del 2019, quando ho iniziato a scrivere questo articolo, ricorreva il 50esimo anniversario della missione Apollo 11 (Neil A. Armstrong, Edwin A. Aldrin and Michael Collins) in cui gli astronauti Armstrong, Aldrin hanno posato il piede sulla superficie lunare. Un evento epocale nella storia umana che segna anche l’inizio della esplorazione spaziale. Dopo 50 anni, la NASA come altre agenzia spaziali e compagnie private, si stanno preparando per tornare sulla Luna per creare avamposti per l’esplorazione umana di pianeti più distanti come per esempio Marte. Questo anniversario mi portò ad interessarmi per raccogleire idee per la mia attività d’insegnamento e per curiosità personale, alle tecniche d’integrazione numerica delle equazioni differenziali usate per effettuare i calcoli delle traiettorie dal sistema di guida delle astronavi Apollo e dai calcolatori che hanno assistito l’impresa dalla Terra. In questo articolo semi divulgativo riassumo le informazione che ho raccolto leggendo (in maniera incompleta) la documentazione della NASA e quella ottenuta leggendo dei libri sull’argomento. Come mio solito presenterò anche dei semplici programmi che implementano questo algoritmi.

L’integrazione numerica nel sistema di guida delle astronavi nelle missioni Apollo

Prima d’inviare la missione Apollo 11sulla Luna, gli scienziati della NASA hanno dovuto affinare la precisione posizione della Luna nella sua orbita usando rivelamenti radar e satellitari. Queste informazioni sono state importantissime per consentire al computer di bordo dei moduli Apollo di effettuare con elevata precisione la navigazione verso la Luna, il corretto inserimento nell’orbita trans lunare, l’allunaggio e le successive fasi del ritorno nell’orbita terrestre. Inoltre, le prime missioni Apollo 8 e 10 hanno fornito dati per ulteriori aggiustamenti che tenevano in conto anche le anomalie gravitazionali lunari sia sia per l’entrata in orbita circumlunare che per la discesa del modulo lunare (LEM). Tutte le missioni Apollo furono dotate di due compatti e all’epoca potenti calcolatori (chiamati Apollo Guidance Computers o AGC) presenti uno nel modulo di comando e uno nel LEM.

Questi miracoli della tecnologia furono ideati nel prestigioso MIT (Massachusetts Institute of Technology). Per ridurre lo spazio furono utilizzati i primi circuiti integrati (la cui commissione della NASA diede un grosso impulso iniziale allo sviluppo e commercializzazione di questa tecnologia) e memorie a nuclei magnetici che garantivano la massima affidabilità nelle condizioni della missione. È stupefacente pensare che questi gioielli d’ingegneria, costati milioni di dollari avessero una potenza di calcolo e una memoria, di poco superiore a uno dei primi home computers (per esempio il Commodore 64) costruiti nel decennio successivo le ultime missioni apollo e commercializzati a un costo un milione di volte inferiore! Come gli home computers degli anni ’80, gli AGC erano dotati di un processore con frequenza di clock di circa 2 MHz. La memoria a sola lettura (ROM) contenente il “sistema operativo” dell’AGC, era chiamata “Core Rope Memory” o “LOL memory” (Little Old Lady memory). Questo tipo di memoria era un sistema di memoria a sola lettura basato su corde intrecciate con fili magnetizzati, e ogni programma era codificato manualmente da un gruppo di donne, che contribuivano a dare il nome “Little Old Lady” alla memoria. La capacità totale della ROM dell’AGC era di circa 36.864 parole di 15 bit ciascuna. Utilizzando la conversione precedentemente menzionata (1,875 byte per parola), puoi calcolare che la ROM dell’AGC era di circa 69.12 kilobyte (36,864 parole x 1,875 byte/parola). L’AGC utilizzava una memoria volatile nota come “Random Access Memory” (RAM). La RAM dell’AGC era divisa in due tipi principali:

Fixed Memory (FMEM): Questa era una forma di RAM non volatire che conservava i dati anche quando il computer era spento. La capacità della FMEM era di 2.048 parole di 16 bit ciascuna.
Erasable Memory (EMEM): Questa era una forma di RAM volatile utilizzata per memorizzare temporaneamente i dati durante l’esecuzione dei programmi. La capacità della EMEM era di 1.024 parole di 16 bit ciascuna.

Usando la conversione di 16 bit per parola (2 byte per parola), puoi calcolare che la capacità totale della RAM dell’AGC (considerando entrambe FMEM ed EMEM) era di circa 6 kilobyte (3,072 parole x 2 byte/parola). Un interessante articolo di B. Hayes sul AGC può essere letto in questo sito [1].

Il software che li controllava era un gioiello d’ingegnosità. Capace di operare in multitasking, era in grado di controllare vari sensori e servo meccanismi in tempo reale. La storia ci insegna che la robustezza di questo programma di controllo venne messa alla prova proprio in occasione del primo allunaggio nel Luglio del 1969. Per un errore (umano), il radar per il rilevamento della posizione del modulo orbitale (CSM) fu lasciato accesso durante la discesa. Durante l’allunaggio, il radar, pur non rilevando il CSM, continuò a innondare di dati la memoria dell’AGC. In risposta, l’AGC avvertì Armstrong e Collins con il famoso codice di allarme 1202, segnalando una sovraccarico della memoria causato dalla frequenza elevata delle letture telemetriche. Tuttavia, pur non sapendo quale fosse esattamente il problema, la NASA diede il consenso a proseguire la missione poiché il sistema operativo poteva superare condizioni di stallo per sopraccarico semplicemente facendo ripartire il computer! Sappiamo bene che per fare ripartire un sistema Window/MacOS/Linux occorre un tempo molto più lungo di una frazione di secondo! Ho cronometrato il reboot del mio MacBook Pro (versione 2012) il cui OS è installato su un disco rigido a stato solido (anche l’AGC usa una memoria allo stato solido ma $2 \times 10^5$ volte meno capiente : 44 secondi. Lascio pensare alle conseguenze di un così lento reboot considerando che il codice di allarme 1202 è apparso diverse volte quando il modulo di allunaggio si trovava a circa 2 km dalla superficie.

Per quanto l’AGC fosse un gioiello di tecnologia, le sue capacità di calcolo erano relativamente limitate dalla sua architettura e fu fatta una scrupolosa scelta degli algoritmi numerici per assicurare l’accuratezza necessaria per le varie fasi della missione. I calcoli più intensivi era quelli di navigazione (in inglese Coasting) in particolare il calcolo della traiettoria di ritorno verso la Terra dall’orbita lunare. Questo calcolo venne effettuato dal AGC presente sul CSM (il computer AGC presente sul LEM era praticamente identico a quello sul CSM). Il calcolo (programma 61) teneva conto della telemetria della astronave e impiegava circa 30 minuti per completarlo. Per questi calcoli era necessario conoscere la posizione della Terra, Sole e Luna rispetto a quello della navicella per poi integrare la traiettoria usando il metodo delle coniche di Milne. Vediamo come.

La traiettoria della luna (e del sole) era memorizzata prima della partenza usando una approssimazione polinomiale del nono grado per ogni coordinata nella forma:

$X(t) = x_0+x_1t+x_2t^2+\cdots x_9t^9$

$Y(t) = y_0+y_1t+y_2t^2+\cdots y_9t^9$

$Z(t) = z_0+z_1t+z_2t^2+\cdots z_9t^9$

In cui, $X(t),zY(t), Z(t)$ forniscono la posizione della luna rispetto alla Terra al tempo $t.$ Quest’ultimo è espresso come la differenza tra il tempo di missione il quello a metà missione [2]. L’approssimazione polinomiale era valida in un intervallo di 15 giorni a partire da poco prima l’inizio della missione (per cui i valori del polinomio non erano memorizzati nella ROM a nuclei magnetici dell’ AGC). L’integrazione delle equazioni del moto venne effettuata usando un metodo di Runge-Kutta [3] nella variazione proposta dal matematico Scandinavo Evert Johannes Nyström nel 1925 [4] e pertanto anche chiamato metodo di Runge-Kutta-Nyström.

I metodi di Runge-Kutta (RK) sono noti per la loro precisione e sono comunemente usati nelle simulazioni numeriche di sistemi dinamici descritti da equazioni differenziali ordinarie (ODE). Rispetto al metodo di Euler, questi metodi ofrono una maggiore precisione e stabilità numerica specialmente per sistemi di ODE con soluzioni oscillanti. Inoltre consentono una maggiore flessibilità nella scelta del passo di integrazione. In alcuni casi, è possibile adattare dinamicamente la lunghezza del passo per gestire meglio regioni del dominio in cui la soluzione varia rapidamente. In fine, nonostante la maggiore complessità rispetto al metodo di Euler, i metodi di RK sono molto usati e ben compresi ed esistono implementazioni robuste, ampiamente disponibili e facili da usare.

Il metodo RK del quarto ordine (RK4) è un algoritmo numerico ampiamente utilizzato per risolvere equazioni differenziali ordinarie (ODE). Questo metodo è più preciso rispetto a metodi di ordine inferiore, come il metodo di Euler, ed è abbastanza efficiente. Ecco una descrizione del metodo:

Supponiamo di avere un’ODE del primo ordine nella forma standard:

$\frac{dy}{dt} = f(t, y)$

dove (y) è la funzione incognita e (f(t, y)) è la funzione che determina il tasso di variazione di (y) rispetto al tempo.

Il metodo di Runge-Kutta del quarto ordine si basa sull’iterazione seguente:

Calcolo dei coefficienti k

$k_1 = h \cdot f(t_n, y_n)$

$k_2 = h \cdot f(t_n + \frac{h}{2}, y_n + \frac{k_1}{2})$

$k_3 = h \cdot f(t_n + \frac{h}{2}, y_n + \frac{k_2}{2})$

$k_4 = h \cdot f(t_n + h, y_n + k_3)$

Dove (h) è la lunghezza del passo dell’iterazione, (t_n) è il tempo corrente, e (y_n) è il valore approssimato di (y) al tempo (t_n).

Calcolo del prossimo valore di (y)

$y_{n+1} = y_n + \frac{1}{6} \cdot (k_1 + 2k_2 + 2k_3 + k_4)$

Questo processo viene quindi ripetuto per avanzare la soluzione temporale. L’indice (n) rappresenta l’iterazione corrente. Il metodo viene facilmente esteso al caso di un sistema dinamico tridimensionale, come la traiettoria deimoduli Apollo nelloo spazio. In questo caso abbiamo un sistema di equazioni differenziali ordinarie (ODE) in x, y, e z in funzione del tempo t del tipo:

$\frac{dx}{dt} = f_1(t, x, y, z)$

$\frac{dy}{dt} = f_2(t, x, y, z)$

$\frac{dz}{dt} = f_3(t, x, y, z)$

dove $f_1(t, x, y, z), f_2(t, x, y, z)$ $f_3(t, x, y, z)$ sono funzioni che descrivono il tasso di variazione rispetto al tempo delle variabili x, y, e z.

Il metodo di Runge-Kutta del quarto ordine può essere adattato per questo sistema come segue:

Calcolo dei coefficienti k

$k_{1x} = h \cdot f_1(t_n, x_n, y_n, z_n)$

$k_{1y} = h \cdot f_2(t_n, x_n, y_n, z_n)$

$k_{1z} = h \cdot f_3(t_n, x_n, y_n, z_n)$

$k_{2x} = h \cdot f_1(t_n + \frac{h}{2}, x_n + \frac{k_{1x}}{2}, y_n + \frac{k_{1y}}{2}, z_n + \frac{k_{1z}}{2})$

$k_{2y} = h \cdot f_2(t_n + \frac{h}{2}, x_n + \frac{k_{1x}}{2}, y_n + \frac{k_{1y}}{2}, z_n + \frac{k_{1z}}{2})$

$k_{2z} = h \cdot f_3(t_n + \frac{h}{2}, x_n + \frac{k_{1x}}{2}, y_n + \frac{k_{1y}}{2}, z_n + \frac{k_{1z}}{2})$

$k_{3x} = h \cdot f_1(t_n + \frac{h}{2}, x_n + \frac{k_{2x}}{2}, y_n + \frac{k_{2y}}{2}, z_n + \frac{k_{2z}}{2})$

$k_{3y} = h \cdot f_2(t_n + \frac{h}{2}, x_n + \frac{k_{2x}}{2}, y_n + \frac{k_{2y}}{2}, z_n + \frac{k_{2z}}{2})$

$k_{3z} = h \cdot f_3(t_n + \frac{h}{2}, x_n + \frac{k_{2x}}{2}, y_n + \frac{k_{2y}}{2}, z_n + \frac{k_{2z}}{2})$

$k_{4x} = h \cdot f_1(t_n + h, x_n + k_{3x}, y_n + k_{3y}, z_n + k_{3z})$

$k_{4y} = h \cdot f_2(t_n + h, x_n + k_{3x}, y_n + k_{3y}, z_n + k_{3z})$

$k_{4z} = h \cdot f_3(t_n + h, x_n + k_{3x}, y_n + k_{3y}, z_n + k_{3z})$

Calcolo dei prossimi valori di x, y, e z

$x_{n+1} = x_n + \frac{1}{6} \cdot (k_{1x} + 2k_{2x} + 2k_{3x} + k_{4x})$

$y_{n+1} = y_n + \frac{1}{6} \cdot (k_{1y} + 2k_{2y} + 2k_{3y} + k_{4y})$

$z_{n+1} = z_n + \frac{1}{6} \cdot (k_{1z} + 2k_{2z} + 2k_{3z} + k_{4z})$

Ogni variabile ha i propri coefficienti k e contribuisce al passo successivo insieme agli altri componenti del sistema. Queste equazioni rappresentano l’estensione delle equazioni del moto per un sistema di corpi con forze centrali in tre dimensioni $(x, y, z).$ Per ogni equazione, le funzioni $f_1(t, x, y, z), f_2(t, x, y, z)$ $f_3(t, x, y, z)$ devono essere specificate in base alla natura specifica del sistema che si sta studiando.

IMPLEMENTAZIONE NEL PROGRAMMA PLANETARIO

Il pezzo di codice che segue in QB64 BASIC calcola le soluzioni approssimate utilizzando il metodo di RK4 e può essere inserito nel progrmma PLANETARIO per la simulazione delle orbite dei pianeti del sistema solare presentato in un precedente articolo (in Inglese).

For K = 1 To N
    MASS(K) = MASS(K) * MU
    X(K) = X1(K) * AU
    Y(K) = Y1(K) * AU
    Z(K) = Z1(K) * AU
    VX(K) = VX1(K) * VCV
    VY(K) = VY1(K) * VCV
    VZ(K) = VZ1(K) * VCV
Next K

' Inizia la simulazione
For T = 1 To NSTEPS
    For I = 1 To N
        ' Runge-Kutta Step 1
        KX1 = VX(I) * DT
        KY1 = VY(I) * DT
        KZ1 = VZ(I) * DT
        KVX1 = AX(I) * DT
        KVY1 = AY(I) * DT
        KVZ1 = AZ(I) * DT

        ' Runge-Kutta Step 2
        X2 = X(I) + 0.5 * KX1
        Y2 = Y(I) + 0.5 * KY1
        Z2 = Z(I) + 0.5 * KZ1
        VX2 = VX(I) + 0.5 * KVX1
        VY2 = VY(I) + 0.5 * KVY1
        VZ2 = VZ(I) + 0.5 * KVZ1
        AX2 = 0
        AY2 = 0
        AZ2 = 0
        For J = 1 To N
            If (J <> I) Then
                D2 = (X2 - X(J)) ^ 2 + (Y2 - Y(J)) ^ 2 + (Z2 - Z(J)) ^ 2
                ID = 1 / Sqr(D2)
                F = G * MASS(J) / D2
                AX2 = AX2 + F * (X(J) - X2) * ID
                AY2 = AY2 + F * (Y(J) - Y2) * ID
                AZ2 = AZ2 + F * (Z(J) - Z2) * ID
            End If
        Next J
        KVX2 = AX2 * DT
        KVY2 = AY2 * DT
        KVZ2 = AZ2 * DT

        ' Runge-Kutta Step 3
        X3 = X(I) + 0.5 * KX2
        Y3 = Y(I) + 0.5 * KY2
        Z3 = Z(I) + 0.5 * KZ2
        VX3 = VX(I) + 0.5 * KVX2
        VY3 = VY(I) + 0.5 * KVY2
        VZ3 = VZ(I) + 0.5 * KVZ2
        AX3 = 0
        AY3 = 0
        AZ3 = 0
        For J = 1 To N
            If (J <> I) Then
                D2 = (X3 - X(J)) ^ 2 + (Y3 - Y(J)) ^ 2 + (Z3 - Z(J)) ^ 2
                ID = 1 / Sqr(D2)
                F = G * MASS(J) / D2
                AX3 = AX3 + F * (X(J) - X3) * ID
                AY3 = AY3 + F * (Y(J) - Y3) * ID
                AZ3 = AZ3 + F * (Z(J) - Z3) * ID
            End If
        Next J
        KVX3 = AX3 * DT
        KVY3 = AY3 * DT
        KVZ3 = AZ3 * DT

        ' Runge-Kutta Step 4
        X4 = X(I) + KX3
        Y4 = Y(I) + KY3
        Z4 = Z(I) + KZ3
        VX4 = VX(I) + KVX3
        VY4 = VY(I) + KVY3
        VZ4 = VZ(I) + KVZ3
        AX4 = 0
        AY4 = 0
        AZ4 = 0
        For J = 1 To N
            If (J <> I) Then
                D2 = (X4 - X(J)) ^ 2 + (Y4 - Y(J)) ^ 2 + (Z4 - Z(J)) ^ 2
                ID = 1 / Sqr(D2)
                F = G * MASS(J) / D2
                AX4 = AX4 + F * (X(J) - X4) * ID
                AY4 = AY4 + F * (Y(J) - Y4) * ID
                AZ4 = AZ4 + F * (Z(J) - Z4) * ID
            End If
        Next J
        KVX4 = AX4 * DT
        KVY4 = AY4 * DT
        KVZ4 = AZ4 * DT

        ' Update positions and velocities using weighted average
        X(I) = X(I) + (1 / 6) * (KX1 + 2 * KX2 + 2 * KX3 + KX4)
        Y(I) = Y(I) + (1 / 6) * (KY1 + 2 * KY2 + 2 * KY3 + KY4)
        Z(I) = Z(I) + (1 / 6) * (KZ1 + 2 * KZ2 + 2 * KZ3 + KZ4)
        VX(I) = VX(I) + (1 / 6) * (KVX1 + 2 * KVX2 + 2 * KVX3 + KVX4)
        VY(I) = VY(I) + (1 / 6) * (KVY1 + 2 * KVY2 + 2 * KVY3 + KVY4)
        VZ(I) = VZ(I) + (1 / 6) * (KVZ1 + 2 * KVZ2 + 2 * KVZ3 + KVZ4)
        If (X(I) < LM And X(I) > -LM) And (Y(I) > -LM And Y(I) < LM) And (Z(I) < LZ And Z(I) > -LZ) Then
            PSet (225 + FX * X(I), 200 + FY * Y(I)), I
            PSet (575 + FX * X(I), 200 + FZ * Z(I)), I
        End If
    Next I

    R = R + DT
    DAYS = R * S2D
    Locate 32, 5: Print Using "TIME LAPSE: ######.## Days -> ####.## Years"; DAYS, DAYS * D2Y
    K$ = InKey$
    If K$ = "E" Or K$ = "e" Then SIGN = 1: RESCALE
    If K$ = "R" Or K$ = "r" Then SIGN = -1: RESCALE
Next T

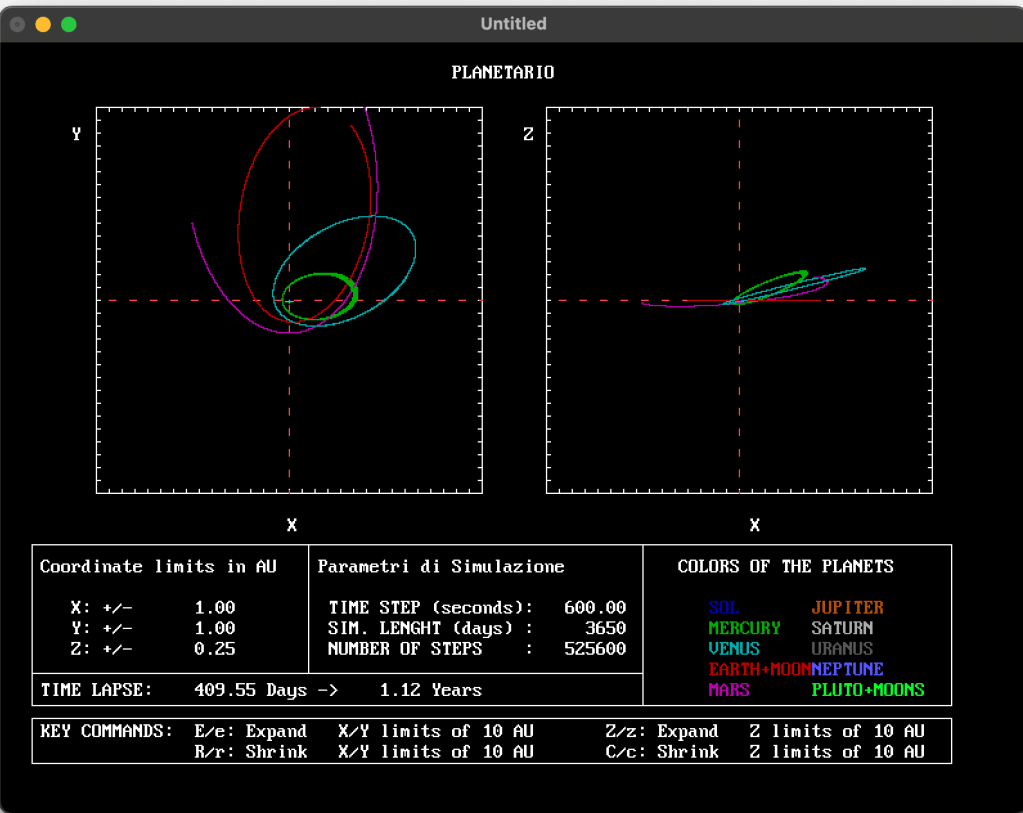
Nella figura che segue è mostrato un esempio di simulazione prodotta dal programma modificato.

"… I seem […] only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me". – Isaac Newton.

Integrazione Numerica di Equazioni Differenziali: 50 anni fa l’uomo ha messo piede sulla Luna. Parte II

IMPLEMENTAZIONE NEL PROGRAMMA PLANETARIO

RIFERIMENTI

Leave a comment Cancel reply

IMPLEMENTAZIONE NEL PROGRAMMA PLANETARIO

RIFERIMENTI

Share this:

Related

Leave a comment Cancel reply