Programming

Numeric Solutions of the Schrödinger equation

/ Danilo Roccatano / Leave a comment

For Schrödinger, the atom was an oscillating system — like the string of a musical instrument — for which there exist a number of modes of oscillation (fundamentals and overtones) which are interpreted as the atom’s energy states.

Armin Hermann. Werner Heisenberg 1901-1976.

This set of slides is from one of my courses in Computational Chemistry. It covers the one-dimensional solution of the Schrödinger equation using Numerov’s method. The material for this article was mainly taken from the excellent Levin textbook in the reference.
If you are interested in more details, please like it and subscribe to my website. This way, I will be motivated to add more of these contents.

Continue reading →

FORTRAN Programming: A Basic Introduction (PART II)

/ Danilo Roccatano / Leave a comment

In college, before video games, we would amuse our- selves by posing programming exercises. One of the favorites was to write the shortest self-reproducing program. Since this is an exercise divorced from reality, the usual vehicle was FORTRAN. Actually, FORTRAN was the language of choice for the same reason that three-legged races are popular.

Ken Thompson, Communications of the ACM. 27 (8), 761–763, 1984.

This is the second part of the basic introductin to FORTRAN programming series.

Control Statements 

Relational operators

Relational operators are used for comparison between variables

< or .lt. : less than 

<= or .le. : less than or equal to 

> or .gt. : greater than 

>= or .ge. :greater than or equal to

== or .eq. : equal to  

/= or .ne. : not equal to

Logical operators

Logical operator are used to perfrom

.and. : Logical multiplication ( and) 

.or. : Logical addition (or) 

.not. : Logical negation (not)

Continue reading →

FORTRAN Programming: A Basic Introduction (PART I)

/ Danilo Roccatano / Leave a comment

In college, before video games, we would amuse our- selves by posing programming exercises. One of the favorites was to write the shortest self-reproducing pro- gram. Since this is an exercise divorced from reality, the usual vehicle was FORTRAN. Actually, FORTRAN was the language of choice for the same reason that three-legged races are popular.

Ken Thompson, Communications of the ACM. 27 (8), 761–763, 1984.

In December of last year, I celebrated the 30th anniversary of my Laurea in Chemistry dissertation. The starting of my thesis dissertation also signed my acquaintance to one of the grannies of the scientific programming languages, FORTRAN. Since then, I have used and (continue to) this language for my research activity by writing several thousands of lines of code. Therefore, I want to share some of my modest programming achievements using this language.

I will concisely introduce this captivating programming language in a series of articles. This is a primer on a programming language with much more to offer, especially in the new versions starting from the FORTRAN 90. Readers interested in deepening their knowledge in FORTRAN can find online many excellent tutorials and discussion groups, as well as plenty of excellent textbooks that have been written.

The FORTRAN language 

Fortran (FORmula TRANslation) language was introduced in 1957 and remains the language of choice for most scientific programming. The language was constantly restyled and updated (e.g. Fortran IV, Fortran 77). Recent improvements, recently introduced with the Fortran 90 and 95/2003, include several extensions in more modern languages (e.g. in the C language). Some of the most important features of Fortran 90/95 include recursive subroutines, dynamic storage allocation and pointers, user-defined data structures, modules, and the ability to manipulate entire arrays. Fortran 90 is compatible with Fortran 77 but not the other way around. However, the new Fortran language has evolved in a modern computer language by incorporating constructs from other languages.  

Continue reading →

A Practical Introduction to the C Language for Computational Chemistry. Part 4

/ Danilo Roccatano / Leave a comment

Controlling complexity is the essence of computer programming.

Brian W. Kernighan. in Software Tools (with PJ Plauger), 1976.

THE FUNCTIONS

A C program is a collection of functions. A C function is equivalent to the subroutine in FORTRAN or BASIC and procedures in PASCAL, PERL, or PYTHON programming languages. A portion of the program cannot be executed independently but only as part of another program. The function contains a specific algorithm or a stand-alone procedure. You have already used several library functions in your previous programs. Output commands for printing or reading files (such as printf(), openf()), mathematical functions (sqrt(), cos() are a library or intrinsic functions as well. Other library functions, we can classify as follows

  • Input/output functions. Input/output on the computer devices (e.g. output to the terminal, printer, hard disk, input from keyboard). It is usually used with #include <stdio.h>;
  • String manipulation functions. This library contains common operations on strings (e.g., concatenation, length, search, and extraction of substrings). It is usually used with #include <string.h>;
  • Mathematical functions. Mathematical calculations (e.g. trigonometrics functions, exponentiation, square root extraction). It is usually used with #include <math.h>;
  • Graphical functions. Function for graphics operations (open a graphical window and canvas) and drawing graphical primitives (e.g. points, line, curves).
  • Operative system control functions. Operation requiriing allocation of the computer resources or devices (e.g. date and time, allocation of memory). It is usually used with, for example, #include <time.h>;
  • Data conversion functions. Operation for data conversion (e.g. change characters type, ascii to integer). It is usually used with #include <ctype.h>;

To use these function, you need to use the precompiler instruction #include at the beginning of the program. The compiler use by deafult the standard library #include <stdlib.h>;

You can write your functions, and it is called user-defined functions. The use of function allows the program to structure and makes its organization and reading easier. C language is structured around the use of functions. The main() function is a function that contains calls to other functions, both intrinsic and user-defined functions.

Continue reading →

NATALE 2022: Il Trigesimo Anniversario della mia Tesi di Laurea

/ Danilo Roccatano / Leave a comment

Mais à l’instant même où la gorgée mêlée des miettes du gâteau toucha mon palais, je tressaillis, attentif à ce qui se passait d’extraordinaire en moi. Un plaisir délicieux m’avait envahi, isolé, sans la notion de sa cause.

PROUST Marcel, Du côté de chez Swann.

Ci sono ricordi del passato che rievocano nostalgicamente piacevoli momenti nella nostra vita. Questi preziosi tesori sono, a volte, sepolti nella nostra mente o, come nel mio caso, in quella di dimenticati cristalli di ferrite. Come per dolcetti di Proust, il ritrovamento di queste vestigie ci fa rivivere le emozioni di un passato lontano. I ricordi di cui parlo sono quelle della mia tesi di Laurea in Chimica che dopo essere stata scritta e discussa fu poi dimenticata nella memoria artificiale di obsoleti supporti magnetici degli albori della rivoluzione digitale.

Discussi la mia tesi di laurea il 23 dicembre dell’anno 1992, era l’ultima sessione di laurea di quell’anno. A quell’epoca, non esisteva ancora la laurea triennale che fu introdotta in conformità con il processo di Bologna dall’anno scolastico 2001/2002. Il corso di laurea in chimica era quinquennale e si entrava in tesi nell’ultimo anno. La tesi sperimentale comportava un lavoro originale che doveva essere discusso di fronte a una commissione di laurea composta dai professori del dipartimento, i relatori e i controrelatori (coloro che dovevano leggere la tesi e valutare il lavoro di ricerca e la sua presentazione). Pertanto, la tesi di Laurea (come del resto l’equivalente tesi magistrale) era un’esperienza molto importante nel condizionare la scelta dello studente nell’avviarsi o meno in una carriera accademica. Nel mio caso, la tesi segnò la scelta di intraprendere la carriera dello scienziato e educatore.  Scelta che, come gli academici goliardici delle prime università europee, mi ha portato a peregrinare lontano dalla mia alma mater nelle lontane Università del nord Europa. Di fatti, questa prefazione è stata abbozzata a Brema in Germania e completata a Lincoln nel Regno Unito, a pochi chilometri dalla città che diede i natali a Isacco Newton.

Continue reading →

Physical Chemistry: The Simple Hückel Method (Part VI): PREVIEW

/ Danilo Roccatano / Leave a comment

LIST OF PREVIOUS LESSONS

Continue reading →

Introduzione alla programmazione in Python (II)

/ Danilo Roccatano / 1 Comment

In questa second parte, continuiamo la nostra esplorazione del linguaggio Python introducedo altri operatori e commandi per manipolare dati.

ESPRESSIONI LOGICHE E OPERATORI

Python dispone di operatori logici che consentono di costruire complesse espressioni logiche.

In Python, le espressioni logiche e gli operatori sono ampiamente utilizzati per la costruzione di complessi algoritmi di controllo di flusso dei dati in un programma.

Continue reading →

Introduzione alla Programmazione in Python

/ Danilo Roccatano / 1 Comment

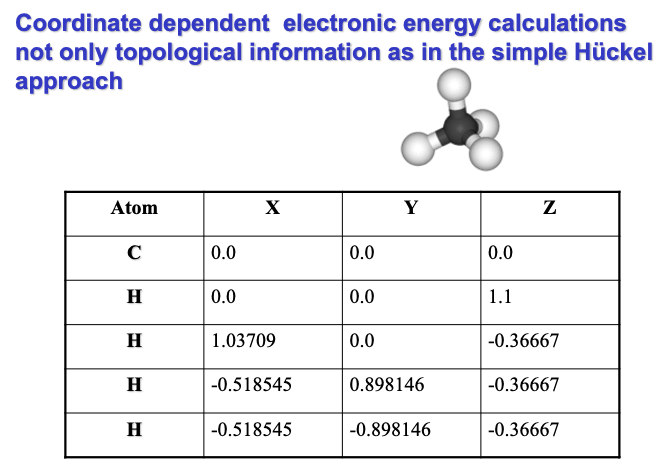
Hi, little cub. Oh, no. Don’t be scared. I’m not gonna hurt you.

Dal film: The Jungle Book. Walt Disney Picture, 2016.

Python è un linguaggio non proprietario e di pubblico dominio è stato creato dall’olandese Guido van Rossum nel 1989. von Rossum racconta nella prefazione che a scritto per il libro sul Python di Lutz e Acher [1], che il progetto di scrivere un nuovo linguaggio è iniziato come un passatempo per le vacanze di Natale! Il linguaggio è stato ispirato dal linguaggio ABC. L’autore dice che “Ho scelto Python come titolo provvisorio per il progetto, essendo di umore un po’ irriverente (e un grande fan di Flying Circus dei Monty Python)”. Sicuramente il risultato è stato un nuovo linguaggio di grandissima diffusine e successo tanto che è tra il linguaggio più usati e insegnati nelle scuole. Il motivo del suo successo è duvuto all’insieme delle caratteristiche che lo distinguono da altri linguaggi di programmazioni che lo hanno preceduto. La sintassi usato per il codice Python è facile da leggere e capire. Permette di ottenere ridurre i tempi di programmazione rendendo possibile scrivere codici complessi in breve tempi. È un linguaggio interpretato ovvero il codice può essere eseguito direttamente senza il bisogno di compilarlo prima. Inoltre, in fase di esecuzione le informazioni ricevute dall’interprete permettono di trovare facilmente errori. Il linguaggio Python può essere usato su tutti i sistemi operativo disponibili quali Windows, Mac, Linux, Android, iOS e anche su microcomputers quali il Raspberry Pi. Sono state sviluppate tantissime raccolte di programmi (chiamate librerie) per eseguire compiti specifici (ad esempio grafica, risoluzione di equazioni differenziali) per velocizzare la scrittura di nuovi programmi.

Python è utilizzato in tutte le area della scienza, tecnologia, attività sociali e finanziarie. Per esempio, è usato nella robotica, per l’analisi dei dati in medicina, astronomia, bioinformatica, fisica delle particelle (solo per citarne alcune), nell’industria cinematografia, musicale e dei videogiochi. 

Pertanto, imparare Python può tornare utile per creare progetti molto interessanti che supportano sia lo studio e che la futura carriera. In questa serie di articoli vengono dati dei rudimenti di programmazione in Python sufficienti a stimolare l’ interesse ad approfondire ulteriormente la conoscenza di questo fantastico linguaggio di programmazione. Per tale scopo si può consultare alla fine di questo articolo un elenco di siti online dove trovare ulteriori informazion sul linguaggio.

Continue reading →

The ROTAforMI: a RObotic TAble for Microscopy

/ Danilo Roccatano / Leave a comment

I have recently published another STEM oriented robotic project. It is the ROTAforMI device, a versatile robotic device for controlling the position and orientation of a microscope slide using four degrees of freedom. This prototype is a complementary development of the idea behind the Roto-microscope project. It was inspired by related projects of servo motors-controlled micromanipulators and 3D micro scanners.

The device is entirely 3D printed and is actioned by four small servos controlled by one Arduino Nano microcontroller. The device can be controlled manually using two micro joysticks (and possibly also automatically via a programmed sequence of movements). In addition, a Bluetooth remote can take snapshots with a smartphone’s camera.

The device is made modular to use for different purposes. For example, removing the Y-stage should be sufficient to fit it under a stereomicroscope. Although the electronic interface is quite bulky, the device is simple to assemble and use, and the controlling program is still in its early stages. The ultimate goal is to use it for automatic photo stacking or 3D image reconstruction. Still, we are sure there are other possible applications in which small motion in 3D dimensions and a rotation of the observation stage can be helpful.

This is a prototype, and there is a lot of space for improvements. So we hope you like it, and constructive comments and suggestions are always welcome!

If you want trying to build one, please follow to the link given above.

Physical Chemistry: The Simple Hückel Method (Part V)

/ Danilo Roccatano / 1 Comment

In the previous four parts of this series of articles on the SHM (the links to the other parts are reported at the end of the article), we learned how to apply the Hückel method to conjugated linear and cyclic molecules containing only carbon atoms. However, an unsaturated molecular system can contain hetero atoms that can conjugate their electrons. The contribution of different theoretical chemists has extended the method by including semiempirical terms for the overlapping integrals that consider the presence of non-carbon atoms in the conjugated system. This effort has been summarized by the American chemist A. Streitwieser providing a set of parameters to approximate both Columb and bond integrals in the Hückel determinant [1]. The derivation of these parameters has been discussed in detail by Streiweiser [2] or by Lowe [2]. This article will teach us how to use these parameters to build up the Hückel determinant for this conjugated molecular system.

Continue reading →