Retro Programming Nostalgia V: Sistemi Autonomi di Equazioni differenziali |

“Qual è l’origine del desiderio, della fascinazione che spinge i fisici, i matematici e presumibilmente anche altri scienziati? La psicoanalisi suggerisce che si tratti di curiosità sessuale. Si comincia chiedendosi da dove vengano i bambini piccoli, una cosa porta all’altra e ci si ritrova a preparare il nitroglicerina o a risolvere equazioni differenziali. Questa spiegazione è un po’ irritante, e quindi probabilmente fondamentalmente corretta.” – David Ruelle, in “Chance and Chaos”

Eccomi di nuovo per un nuovo appuntamento con la versione in italiano della Rubrica “Retro Programming Nostalgia “, la mia personalissima avventura d’ archeologia informatica alla riscoperta di vecchi programmi scritti qualche tempo fa su microcomputers che hanno segnato un’epoca.

Questa volta, nei miei vecchi dischetti per il glorioso Amiga 500, ho trovato un programma in Amiga Basic che scrissi durante i primi anni dei miei studi universitari, quando studiavo nel corso di matematica II, i sistemi d’equazioni differenziali. In particolare, ero molto affascinato dai sistemi di equazioni differenziali autonomi per via delle molteplici applicazioni nella modellazione matematica di sistemi fisici, chimici e biologici, e per la loro importanza nella teoria del caos. Come negli articoli della serie, voglio rilasciare una versione riadattata per il meta compilatore QB64 BASIC, ma prima di presentare il programma, voglio brevemente spiegare cosa sia un sistema autonomo di equazioni differenziali.

I sistemi autonomi d’equazioni differenziali

In matematica, si definisce “autonomo” un sistema di equazioni differenziali che non dipende esplicitamente dal tempo. Se il sistema dipende solo da due variabili dipendenti (o di stato), allora viene anche chiamato “piano” poiché le soluzioni di queste variabili possono essere visualizzate in un piano bidimensionale.

Matematicamente, un sistema autonomo di questo tipo è definito come:

$\begin{cases} \frac{dx}{dt} = f(x, y) \\ \frac{dy}{dt} = g(x, y) \end{cases}$

con x e y le variabili di stato e le derivative $dx/dt$ e $dy/dt$ le loro variazione rispetto alla variabile t. Le funzioni f(x, y) e g(x, y) determinano le relazioni tra le derivative e le variabili di stato. Queste funzioni possono dipendere linearmente o nonlinearmente da x e y (o essere semplicemente delle costanti), ma non coinvolgono esplicitamente la variabile indipendente (in questo caso t).

Il comportamento di un sistema del genere può essere estremamente affascinante e ricco, passando da punti di equilibrio stabili, orbite periodiche, comportamenti caotici e altro ancora. Matematici e scienziati spesso utilizzano tecniche grafiche e metodi analitici per studiare le proprietà e le soluzioni dei sistemi piani autonomi, acquisendo approfondimenti sul loro comportamento a lungo termine. Questi sistemi trovano applicazioni in vari campi, tra cui fisica, ingegneria, biologia ed economia, per modellare e comprendere la dinamica di vari fenomeni del mondo reale. In generale, i sistemi autonomi di equazioni differenziali piane sono strumenti essenziali nello studio dei sistemi dinamici (dipendenti dal tempo) e forniscono preziose informazioni sul evoluzione di sistemi fisici complessi nel tempo.

Andiamo più in profondità nell’argomento esplorando i cosiddetti punti critici e il tipo di soluzioni di questi sistemi.

Punti Critici (Punti di Equilibrio)

In un sistema planare autonomo, i punti critici, anche noti come punti di equilibrio o punti fissi, sono i punti in cui le derivate di entrambe le variabili di stato rispetto al tempo sono uguali a zero. Matematicamente, per un sistema con le variabili di stato x e y, i punti critici sono trovati risolvendo le seguenti equazioni simultaneamente:

$\begin{cases} f(x, y)=0 \\ g(x, y)=0 \end{cases}$

I punti critici rappresentano stati in cui il sistema si trova in uno stato stazionario, il che significa che le variabili di stato non cambiano nel tempo. Questi punti sono cruciali in quanto rivelano comportamenti stabili, instabili o semi-stabili del sistema. Il comportamento attorno ai punti critici può essere determinato analizzando gli autovalori della matrice jacobiana del sistema valutata in quei punti.

Analisi del piano di fase

Per ottenere una comprensione più approfondita del comportamento di un sistema planare autonomo, si utilizza comunemente l’analisi del piano di fase. Il piano di fase rappresenta le traiettorie del sistema nello spazio degli stati (piano). Ogni asse rappresenta una delle variabili di stato, e le traiettorie vengono rappresentate come curve su questo piano.

Tracciando i punti critici e analizzando le loro proprietà di stabilità, oltre a disegnare alcune traiettorie tipiche, si può visualizzare il comportamento complessivo del sistema e individuare importanti caratteristiche come cicli limite, punti fissi e dinamiche complesse.

In sintesi, i sistemi autonomi di equazioni differenziali planari svolgono un ruolo cruciale nella comprensione della dinamica di vari sistemi del mondo reale. Studiando i punti critici e analizzando le soluzioni, matematici e scienziati possono acquisire conoscenze sul comportamento a lungo termine di questi sistemi, aiutandoli a fare previsioni e trarre conclusioni sulle fenomenologie che rappresentano.

I sistemi autonomi di equazioni differenziali planari presentano vari comportamenti affascinanti, rendendoli un’area ricca di studi per matematici e scienziati. Ecco alcuni approfondimenti sui diversi tipi di comportamenti osservati in tali sistemi.

Punti di Equilibrio Stabili: Un punto di equilibrio stabile, noto anche come attrattore, rappresenta uno stato in cui il sistema tende a stabilizzarsi nel tempo. Se le traiettorie del sistema iniziano vicino a un punto di equilibrio stabile, convergeranno verso di esso man mano che il tempo passa. Tali punti sono importanti per capire il comportamento in stato stazionario del sistema e possono corrispondere a stati stabili in sistemi fisici, come la posizione di riposo di un pendolo o il punto di equilibrio di una reazione chimica.
Punti di Equilibrio Instabili: Un punto di equilibrio instabile, chiamato anche repellente, rappresenta uno stato in cui il sistema è altamente sensibile alle perturbazioni. Le traiettorie che iniziano vicino a un punto instabile si allontanano rapidamente da esso nel corso del tempo. Questi punti spesso corrispondono a stati instabili o condizioni critiche in sistemi reali.
Punti di Sella: Un punto di sella è un tipo speciale di punto critico che presenta comportamenti stabili e instabili lungo diverse direzioni nello spazio degli stati. Le traiettorie vicine a un punto di sella si avvicinano ad esso in una direzione e si allontanano nell’altra. I punti di sella sono interessanti perché rappresentano una combinazione di stabilità e instabilità e la loro presenza può portare a dinamiche complesse nel sistema.
Cicli Limite: Un ciclo limite è una traiettoria chiusa nel piano delle fasi che il sistema segue ripetutamente senza avvicinarsi a un punto critico. Questi cicli corrispondono a comportamenti periodici o oscillatori nel sistema. I cicli limite possono essere stabili, portando a oscillazioni regolari e prevedibili, o instabili, risultando in oscillazioni non ripetibili.

Complessivamente, lo studio dei sistemi autonomi di equazioni differenziali piane è un campo affascinante e interdisciplinare che combina l’analisi matematica, i metodi numerici e le tecniche grafiche. Comprendere i comportamenti e le proprietà di questi sistemi aiuta scienziati e ingegneri a comprendere la dinamica di fenomeni complessi, progettare strategie di controllo e fare previsioni su processi del mondo reale. L’interazione tra stabilità, periodicità, caos e biforcazioni rende questa area di ricerca sia stimolante che gratificante, con numerose applicazioni in diverse discipline scientifiche.

Le Soluzioni (Traiettorie nello spazio delle fasi)

Le soluzioni di un sistema planare autonomo sono le curve che descrivono come le variabili di stato si evolvono nel tempo. Risolvere tali sistemi non è sempre semplice e soluzioni analitiche potrebbero non esistere per tutti i casi. Tuttavia, i metodi numerici, come il metodo di Eulero o il metodo di Runge-Kutta, possono approssimare le soluzioni numericamente. Ci sono diversi tipi di soluzioni o traiettorie che il sistema può mostrare:

Soluzioni stabili: Se le traiettorie vicine convergono verso un punto critico nel corso del tempo, il punto critico è considerato stabile. Il sistema tende a tornare a questo stato dopo piccole perturbazioni.
Soluzioni instabili: Se le traiettorie vicine divergono da un punto critico, il punto critico è instabile. Anche piccole perturbazioni possono allontanare il sistema da questo stato.
Soluzioni semistabili: Un punto critico semistabile può avere un comportamento stabile in una direzione e un comportamento instabile in un’altra direzione.
Cicli limite: Si tratta di traiettorie chiuse e periodiche che il sistema segue indefinitamente senza avvicinarsi a un punto critico. I cicli limite spesso rappresentano un comportamento periodico o oscillatorio nel sistema.
Chaos: In alcuni casi, il sistema può mostrare un comportamento caotico, in cui le traiettorie sono estremamente sensibili alle condizioni iniziali, risultando in modelli imprevedibili e non ripetitivi.

STUDIO DI UN SISTEMA AUTONOMO PIANO LINEARE

Consideriamo il sistema autonomo planare:

$\begin{cases} \frac{dx}{dt} = ax+by \\ \frac{dy}{dt} = cx+dy \end{cases}$

dove a, b, c e d sono costanti.

Per eseguire un’analisi del piano di fase, troveremo i punti critici e classificheremo la loro stabilità, quindi tracceremo alcune traiettorie tipiche per visualizzare il comportamento del sistema.

Trovare i punti critici
I punti critici vengono trovati impostando le derivate dx/dt e dy/dt uguali a zero:

$\begin{cases} ax+by=0 \\ cx+dy=0 \end{cases}$

Per trovare i punti critici $(x_c, y_c)$ , risolviamo il sistema di equazioni. Supponiamo che $a \neq d$ per evitare casi degeneri:

Dalla prima equazione, possiamo isolare y:

$y = -(a/b) x$

Ora, sostituisci questo valore di y nella seconda equazione:

$cx + d(-(a/b) x) = 0$

Successivamente, isola x:

$x(c - (ad/b)) = 0$

Quindi, abbiamo due punti critici:

$x = 0$
$x = b/d$ (assumendo che $c \neq (ad/b)$ )

Utilizzando la relazione $y = -(a/b) x$ , possiamo trovare i corrispondenti valori di y per questi punti critici:

$(0, 0)$
$(b/d, -a/d)$

Analisi di stabilità
Per analizzare la stabilità dei punti critici, è necessario calcolare la matrice jacobiana valutata in ogni punto critico. La matrice jacobiana per il sistema bidimensional è:

$J=\left| \begin{array}{cc} \frac{\partial (dx/dt)}{\partial x} & \frac{\partial (dx/dt)}{\partial y} \\ \frac{\partial (dy/dt)}{\partial x} & \frac{\partial (dy/dt)}{\partial y} \end{array} \right|$

Dove ∂ rappresenta la derivata parziale. In questo caso, il comportamento del sistema è riassunto nel grafico del determinante rispetto alla traccia di J.

Nel caso del sistemi autonomo lineare considerato nel precedente paragrafo, il Jacobiano è definito come:

$J=\left| \begin{array}{cc} a & b \\ c & d \end{array} \right|=(ad-bc)$

Ora, valutiamo la matrice jacobiana in ogni punto critico:

At (0, 0):

$J(0,0)=\left| \begin{array}{cc} a & b \\ c & d \end{array} \right|$

At (b/d, -a/d):

$J(b/d, -a/d)=\left| \begin{array}{cc} a & b \\ c & d \end{array} \right|$

Rappresentazione e classificazione delle traiettorie nello spazio delle fasi
Siamo arrivati al punto in cui l’uso di un programma per calcolatore può essere molto utile la visualizzazione delle soluzioni di questi sistemi. Per disegnare alcune traiettorie tipiche per visualizzare il comportamento del sistema nel piano di fase possiamo prima individuare i punti critici (0, 0) e (b/d, -a/d) e poi disegnare traiettorie rappresentative attraverso diverse condizioni iniziali.

La direzione delle traiettorie può essere determinata dai segni di dx/dt e dy/dt. Ad esempio, se dx/dt > 0 e dy/dt > 0 in un certo punto (x, y), allora la traiettoria punta al quadrante in alto a destra da quel punto.

La forma e il comportamento effettivi delle traiettorie dipendono dai valori specifici di a, b, c, e d. Analizzando la stabilità dei punti critici, possiamo dedurre se le traiettorie convergono verso o si allontanano da questi punti.

La classificazione delle soluzioni in un sistema autonomo di equazioni differenziali planari coinvolge la comprensione del comportamento delle traiettorie intorno ai punti critici. La classificazione si basa sulle proprietà di stabilità di questi punti critici, che possono essere classificati in tre categorie principali:

Punti critici stabili (Attrattori):
Un punto critico $(x_c, y_c)$ è considerato stabile se le traiettorie che partono nelle sue vicinanze convergono verso il punto critico con il passare del tempo. In altre parole, se si introduce una piccola perturbazione (deviazione iniziale) alle variabili di stato (x, y) intorno al punto critico, le traiettorie alla fine si avvicineranno e rimarranno vicine al punto critico. I punti critici stabili sono spesso associati a comportamenti stabili e prevedibili nel sistema. Ad esempio, nel contesto di un sistema meccanico, un punto critico stabile potrebbe rappresentare la posizione di equilibrio in cui il sistema si stabilisce quando non viene disturbato.

Punti critici instabili (Repellers):
Un punto critico $(x_c, y_c)$ è considerato instabile se le traiettorie che partono nelle sue vicinanze si allontanano dal punto critico con il passare del tempo. In questo caso, piccole perturbazioni alle variabili di stato fanno sì che le traiettorie si allontanino sempre di più dal punto critico. I punti critici instabili rappresentano stati o condizioni instabili nel sistema. Ad esempio, in un sistema meccanico, un punto critico instabile potrebbe corrispondere alla posizione di un pendolo invertito, dove il minimo disturbo porta al crollo.

Punti di sella:
Un punto di sella è un tipo speciale di punto critico che mostra comportamenti stabili e instabili lungo diverse direzioni nello spazio di stato. Le traiettorie vicino a un punto di sella si avvicinano al punto critico lungo una direzione (stabile) e si allontanano da esso lungo un’altra direzione (instabile). I punti di sella si caratterizzano per avere almeno un autovalore positivo e un autovalore negativo nella loro matrice

In un sistema planare autonomo di equazioni differenziali del tipo:

$\begin{cases} \frac{dx}{dt} = ax+by \\ \frac{dy}{dt} = cx+dy \end{cases}$

Le caratteristiche delle soluzioni del sistema dipendono dalle proprietà della matrice dei coefficienti ( $\begin{bmatrix} a & b \ c & d \end{bmatrix}$ ). In particolare, è possibile ottenere varie tipologie di soluzioni in base al traccia e al determinante di questa matrice, ossia $Tr=(a+b)$ e $Det=(ad-bc).$

Classificazione delle Soluzioni in Base alla Matrice dei Coefficienti

A. Determinante e Traccia entrambi positivi ((ad – bc > 0) e (a + d > 0)):
- Questo indica che la matrice ha due autovalori reali e di segno opposto.Le soluzioni del sistema convergono a un punto stabile nell’origine (un punto di equilibrio asintoticamente stabile).
B. Determinante e Traccia entrambi negativi ((ad – bc > 0) e (a + d < 0)):
- La matrice ha due autovalori reali di segno opposto.Le soluzioni del sistema convergono a un punto stabile nell’origine (un punto di equilibrio asintoticamente stabile), ma seguono traiettorie oscillanti.
C. Determinante positivo, Traccia negativa ((ad – bc > 0) e (a + d < 0)):
- La matrice ha due autovalori complessi con parte reale negativa.Le soluzioni del sistema convergono a un punto stabile nell’origine, seguendo traiettorie oscillanti.
D. Determinante nullo ((ad – bc = 0)):
- In questo caso, la matrice ha un autovalore reale doppio o due autovalori coincidenti.Le soluzioni possono essere lineari o avere comportamenti speciali, come traiettorie radiali o circolari.
E. Determinante negativo ((ad – bc < 0)):
- La matrice ha due autovalori complessi con parte reale non nulla.
- Le soluzioni seguono traiettorie spiraliformi, avvicinandosi o allontanandosi da un punto stabile nell’origine a seconda del segno della parte reale degli autovalori.
Determinante Nullo o Autovalori Multipli: Quando il determinante è nullo o ci sono autovalori multipli, le soluzioni possono comportarsi in modi più complessi. In questi casi, è necessario considerare ulteriori dettagli, come l’analisi degli autovalori e degli autovettori, per determinare il comportamento esatto del sistema.

In Appendice ho riportato il programma di cui parlavo all’inizio dell’articolo. Il programma è stato al compilatore BASIC QB64 adattato e anche migliorato. Il programma permetted di cambiare i parametri e cliccando sul grafico ottenere le soluzioni per valori iniziali di $(x_0,y_0)$ . E’ possible anche scansionare lungo x e Y per ottere automaticamente un set di curve equispaziate.

Nelle figure che seguono sono riportati alcuni esempi di rappresentazioni del piano di fase per diversi systemi.

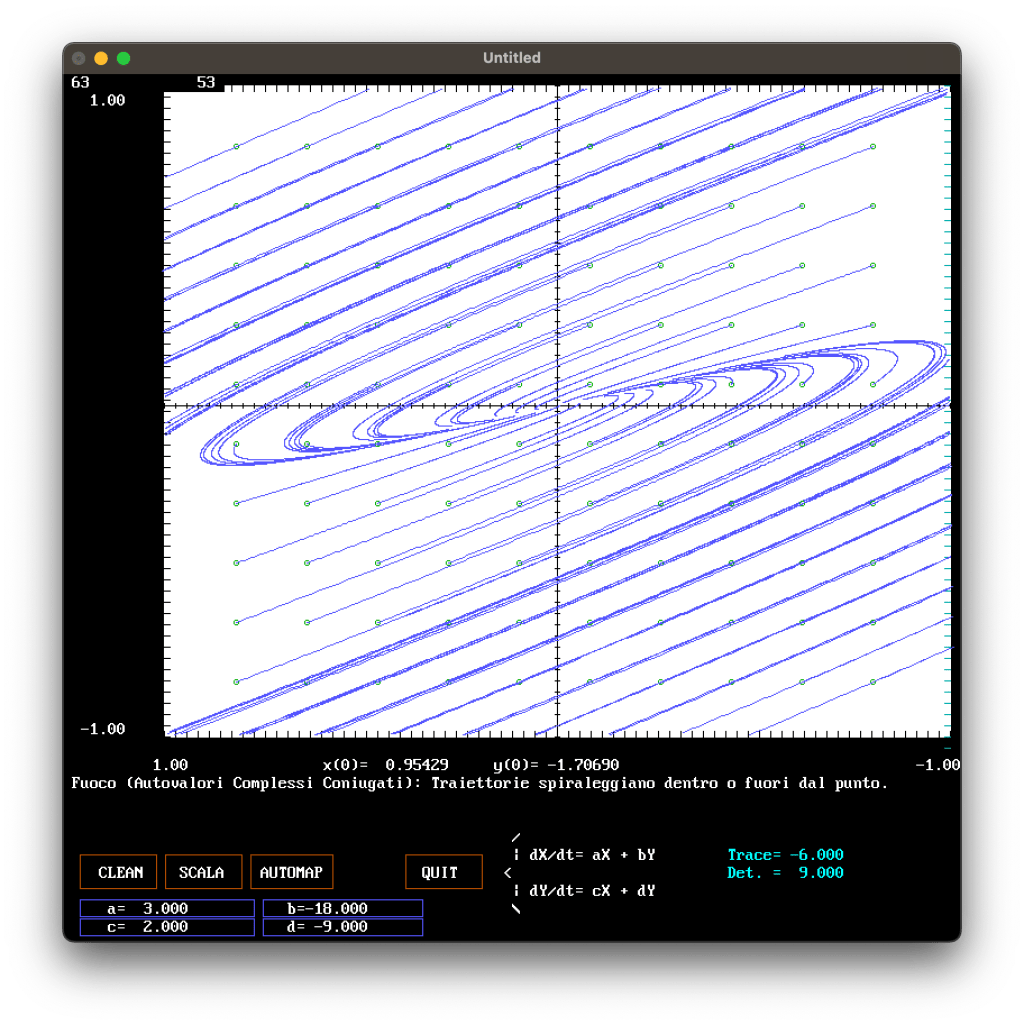
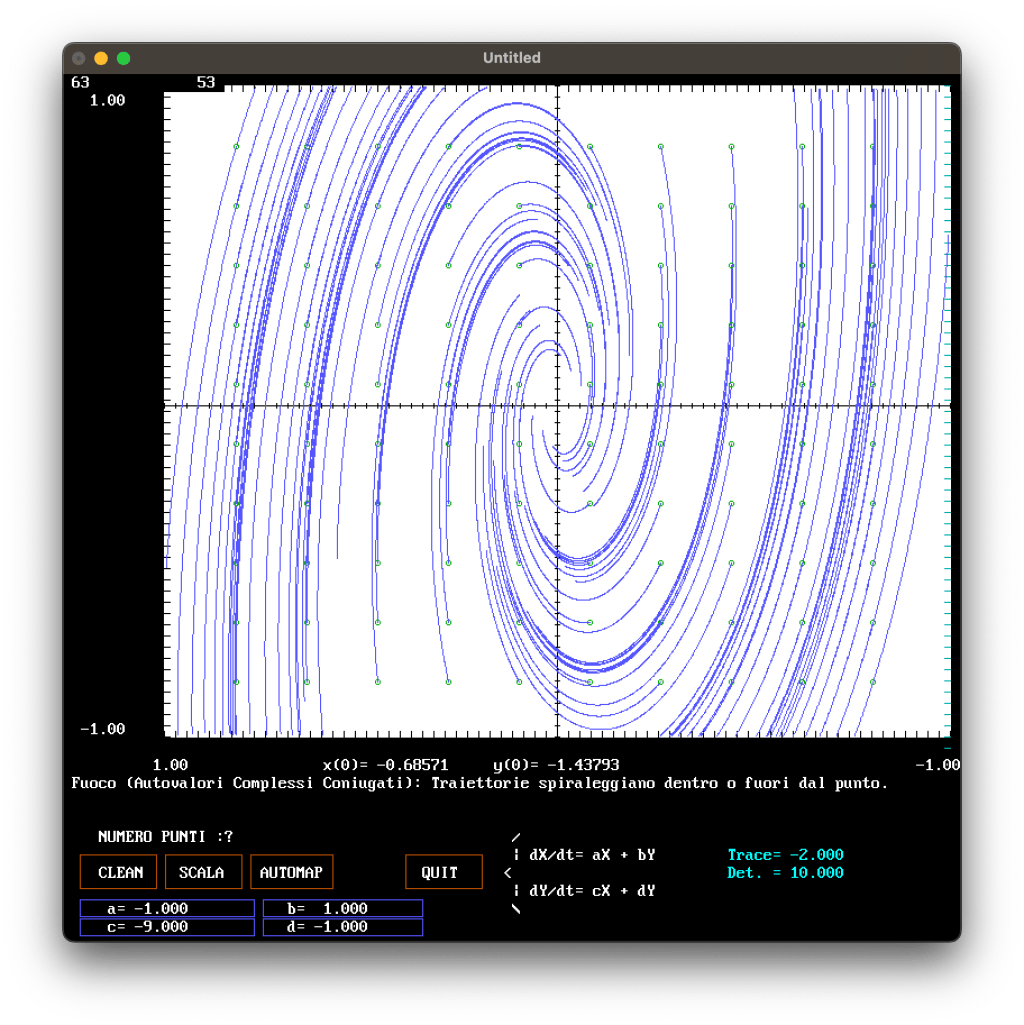
APPENDICE

Il programma in QB64 Basic (Qbasis) per lo studio di un systema di DE autonomo piano lineare. Questo programma è strumento interattivo per visualizzare e analizzare il comportamento delle soluzioni di un sistema di equazioni differenziali ordinarie lineari. Gli utenti possono regolare i parametri del sistema, eseguire simulazioni e ottenere informazioni sulla classificazione dei punti critici.

Ecco una breve descrizione delle parti principali del programma:

DISEGNA_INTER:

Questa subroutine disegna un’interfaccia grafica per visualizzare il sistema di equazioni differenziali.
Disegna assi cartesiani, linee guida e fornisce informazioni sulla scala e sui parametri del sistema.
In base ai valori dei coefficienti a, b, c, e d, classifica il comportamento del punto critico del sistema.

ClassifyCriticalPoint:

Questa subroutine viene chiamata da DISEGNA_INTER per classificare il punto critico del sistema in base ai valori di traccia (Tr) e determinante (Det) della matrice dei coefficienti.
Fornisce una descrizione testuale del tipo di punto critico e stampa i valori di traccia e determinante.

MAIN:

La subroutine principale del programma gestisce l’interazione con l’utente e il controllo del mouse.
Permette all’utente di modificare i parametri del sistema, di pulire il grafico, di regolare la scala e di eseguire una simulazione delle traiettorie del sistema.

INTEGRAZIONE_EUL:

Questa subroutine esegue l’integrazione numerica delle equazioni differenziali utilizzando il metodo di Eulero.
Calcola e traccia le traiettorie nel grafico in base ai parametri del sistema e alla posizione del mouse.

Si prega di leggere in questo link le condizioni di utilizzo del programma.

''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''
'          STUDIO DEL SISTEMA DI EQUAZIONI DIFFERENZIALI
'           AUTONOMO  PIANO LINEARE     
'          
 '        | dX/dt= aX + bY "
 '     < 
 '       | dY/dt= cX + dY "
'          
'           VERSIONE:     1.1                 '
'
'          AUTORE: (C) DANILO ROCCATANO   1993
'         PRIMA VERSIONE: 1993
'         REVISIONE: 2023
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''

Screen _NewImage(800, 800, 256)
Dim Shared a, b, c, d, dx, dy As Double
Dim Shared h As Double
Dim Shared pa, PX, PY, CL As Integer
Dim Shared EINFX, ESUPX, EINFY, ESUPY As Double

a = 1
b = 2
c = 3
d = 1

' Limiti iniziali del grafico
EINFX = -1.
ESUPX = 1.0
EINFY = -1.0
ESUPY = 1.0

Cls
DISEGNA_INTER

MAIN

Sub INPUT_PAR
    Shared a, b, c, d, dx, dy
    Shared h
    Shared pa, PX, PY
    Dim pp As Double

    Locate 43, 5: Input "INSERISCI PARAMETRO:"; pp
    If pa = 1 Then a = pp
    If pa = 2 Then b = pp

    If pa = 7 Then c = pp
    If pa = 8 Then d = pp

    pa = 0
    Cls
    DISEGNA_INTER

End Sub

Sub DISEGNA_INTER
    Shared a, b, c, d, dx, dy
    Shared h
    Shared pa

    Line (90, 10)-(790, 590), 3, B
    Line (90, 10)-(790, 590), 15, BF

    Line (440, 10)-(440, 610), 0
    Line (90, 295)-(790, 295), 0
    For T = 0 To 80
        Line (90 + 10 * T, 293)-(90 + 10 * T, 297), 0
        Line (90 + 10 * T, 10)-(90 + 10 * T, 15), 0
        Line (90 + 10 * T, 585)-(90 + 10 * T, 590), 0
    Next T
    For T = 0 To 60
        Line (90, 10 + 10 * T)-(95, 10 + 10 * T), 0
        Line (438, 10 + 10 * T)-(442, 10 + 10 * T), 0
        Line (785, 10 + 10 * T)-(790, 10 + 10 * T), 3
    Next T
    Locate 2, 2: Print Using "###.##"; ESUPY
    Locate 37, 2: Print Using "###.##"; EINFY
    Locate 39, 9: Print Using "###.##"; ESUPX
    Locate 39, 95: Print Using "###.##"; EINFX

    ' MENU DEI COMMANDI
    Locate 45, 4: Print " CLEAN   "
    Locate 45, 12: Print "  SCALA "
    Locate 45, 22: Print " AUTOMAP"
    Locate 45, 40: Print " QUIT    "

    Line (15, 695)-(83, 725), 6, B
    Line (91, 695)-(159, 725), 6, B
    Line (167, 695)-(240, 725), 6, B
    Line (305, 695)-(373, 725), 6, B

    Locate 43, 50: Print " /"
    Locate 44, 50: Print " | dX/dt= aX + bY "
    Locate 45, 50: Print "< "
    Locate 46, 50: Print " | dY/dt= cX + dY "
    Locate 47, 50: Print " \"

    Locate 47, 5: Print " a=                  b=            "
    Locate 48, 5: Print " c=                  d=            "

    Locate 47, 8: Print ; Using "##.###"; a
    Locate 47, 28: Print ; Using "##.###"; b

    Line (15, 735)-(170, 750), 9, B
    Line (178, 735)-(320, 750), 9, B

    Locate 48, 8: Print ; Using "##.###"; c
    Locate 48, 28: Print ; Using "##.###"; d

    Line (15, 752)-(170, 767), 9, B
    Line (178, 752)-(320, 767), 9, B

    Tr = a + d
    Det = a * d - b * c

    ' Classify the critical point
    ClassifyCriticalPoint Tr, Det

End Sub

' Subroutine per classificare le solutzioni e punti critici sulla base della traccia e del determinante 
' della matrice dei coefficienti.

Sub ClassifyCriticalPoint (T, D)

    If T > 0 And D > 0 Then
        TEXT$ = "Nodo (Autovalori Reali Distinti): Traiettorie convergono (Stabile o Instabile)."
    ElseIf T > 0 And D < 0 Then
        TEXT$ = "Punto di Sella (Autovalori Reali Distinti): Traiettorie si avvicinano in una direzione e si allontanano in un'altra (Instabile)."
    ElseIf T < 0 And D > 0 Then
        TEXT$ = "Fuoco (Autovalori Complessi Coniugati): Traiettorie spiraleggiano dentro o fuori dal punto."
    ElseIf T = 0 And D > 0 Then
        TEXT$ = "Centro (Autovalori Complessi Coniugati): Traiettorie formano orbite chiuse."
    ElseIf T = 0 And D = 0 Then
        TEXT$ = "Centro (Autovalori Complessi Coniugati): Traiettorie formano orbite chiuse."
    ElseIf T = 0 And D > 0 Then
        TEXT$ = "Nodo o Stella Degenerati (Autovalori Reali Distinti): Traiettorie convergono o si allontanano."
    ElseIf T = 0 And D < 0 Then
        TEXT$ = "Punto di Sella Degenerato (Autovalori Reali Distinti): Traiettorie si avvicinano in una direzione e si allontanano in un'altra (piu' lentamente rispetto a un punto di sella regolare)."
    Else
        TEXT$ = "Imprevedibile (Autovalori Complessi Coniugati): Il comportamento puo' essere imprevedibile, coinvolgendo oscillazioni complesse o caos."
    End If
    Locate 40, 2: Print TEXT$
    Color 11: Locate 44, 75: Print ; Using "Trace=###.###"; Tr
    Locate 45, 75: Print ; Using "Det. =###.###"; Det

End Sub


Sub MAIN
    Shared a, b, c, d, dx, dy
    Shared h
    Shared pa, PX, PY, CL As Integer

    'x-y range
    DELTAX = ESUPX - EINFX
    DELTAY = ESUPY - EINFY

    'integration step
    h = 0.01
    fs = 1
    ' risoluzione
    dx = DELTAX / 700
    dy = DELTAY / 580

    ' Controllo del mouse
    Do
        Do While _MouseInput
            ta = _MouseButton(1)
            mx = _MouseX
            my = _MouseY
            ' Posizione relativa del pixel
            X0 = (mx - 400) * dx
            Y0 = (295 - my) * dy
            'Coordinate cartesiane della posizione del puntatore
            Locate 39, 30: Print Using "x(0)=###.#####     y(0)=###.#####"; X0, Y0

            If (ta And my <= 590 And mx >= 90 And mx <= 790) Then
                PX = mx
                PY = my
                CL = 6
                INTEGRAZIONE_EUL
                ta = 0
            End If

            'Controlla se il mouse si trova nella prima linea dei parametri
            If (ta And my >= 735 And my <= 750) Then
                If (mx >= 15 And mx <= 170) Then pa = 1
                If (mx >= 178 And mx <= 320) Then pa = 2
                INPUT_PAR
                ta = 0
            End If

            If (ta And my >= 752 And my <= 767) Then
                If (mx >= 15 And mx <= 170) Then pa = 7
                If (mx >= 178 And mx <= 320) Then pa = 8
                INPUT_PAR
                ta = 0
            End If

            Line (15, 695)-(83, 725), 6, B
            Line (91, 695)-(159, 725), 6, B
            Line (167, 695)-(240, 725), 6, B

            If (ta And my >= 695 And my <= 734) Then
                ky$ = "0"
                If (mx >= 15 And mx <= 83) Then ky$ = "1"
                If (mx >= 91 And mx <= 159) Then ky$ = "2"
                If (mx >= 167 And mx <= 240) Then ky$ = "3"
                If (mx >= 305 And mx <= 373) Then ky$ = "4"

                Select Case ky$
                    Case "1"
                        Cls
                        DISEGNA_INTER
                    Case "2"
                        KK = fs
                        Locate 43, 5: Input "Fattore di scala:"; fs
                        If sf < 0 Then
                            fs = KK
                        End If
                        If KK <> fs Then
                            Cls
                            DISEGNA_INTER
                        End If
                        EINFX = EINFX * fs
                        ESUPX = ESUPX * fs
                        EINFY = EINFY * fs
                        ESUPY = ESUPY * fs
                        DELTAX = ESUPX - EINFX
                        DELTAY = ESUPY - EINFY
                        Locate 43, 5: Print Space$(40)
                    Case "3"
                        Locate 43, 5: Input "NUMERO PUNTI :"; PUNTI%
                        Locate 43, 5: Print Space$(40)
                        ' Curve campionate lungo X in verde
                        CL = 2
                        For T = 0 To PUNTI%
                            PX = (700 / PUNTI%) * T
                            PY = 295
                            INTEGRAZIONE_EUL
                        Next T
                        ' Curve campionate lungo Y in blue
                        CL = 9
                        For T = 0 To PUNTI%
                            PX = 440
                            PY = (590 / PUNTI%) * T
                            INTEGRAZIONE_EUL
                        Next T
                        ta = 0
                    Case "4"
                        End
                End Select
                ta = 0
            End If
        Loop
    Loop
End Sub

Sub INTEGRAZIONE_EUL
    Shared a, b, c, d, dx, dy As Double
    Shared h
    Shared pa, PX, PY, CL As Integer

    PSet (PX, PY), CL
    mx = PX - 440
    my = 295 - PY
    X0 = mx * dx
    Y0 = my * dy

    jj = 1
    XP = X0
    YP = Y0
    nn = 0
    Do While nn < 701

        ' Sistema

        INX = jj * h * (a * XP + b * YP)
        INY = jj * h * (b * XP + c * YP)


        X = XP + INX
        Y = YP + INY
        XP = X
        YP = Y

        PX = X / dx + 440
        PY = 295 - Y / dy

        If (PX >= 790 Or PX <= 90) Or (PY <= 10 Or PY >= 590) Then
            If jj = 1 Then
                jj = -1
                X = X0
                Y = Y0
                PSet (PX, PY), CL
            Else
                jj = 1
                Exit Sub
            End If
        End If
        Locate 39, 30: Print Using "x=   ###.#####     y=   ###.#####"; X0, Y0
        Line -(PX, PY), CL
        nn = nn + 1
    Loop
End Sub

"… I seem […] only like a boy playing on the sea-shore, and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary, whilst the great ocean of truth lay all undiscovered before me". – Isaac Newton.

Retro Programming Nostalgia V: Sistemi Autonomi di Equazioni differenziali

I sistemi autonomi d’equazioni differenziali

Punti Critici (Punti di Equilibrio)

Analisi del piano di fase

Le Soluzioni (Traiettorie nello spazio delle fasi)

Classificazione delle Soluzioni in Base alla Matrice dei Coefficienti

APPENDICE

Leave a comment Cancel reply

I sistemi autonomi d’equazioni differenziali

Punti Critici (Punti di Equilibrio)

Analisi del piano di fase

Le Soluzioni (Traiettorie nello spazio delle fasi)

Classificazione delle Soluzioni in Base alla Matrice dei Coefficienti

APPENDICE

Share this:

Related

Leave a comment Cancel reply